题目内容
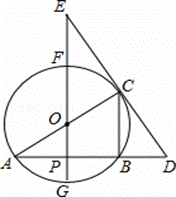
如图,⊙O中,FG、AC是直径,AB是弦,FG⊥AB,垂足为点P,过点C的直线交AB的延长线于点D,交GF的延长线于点E,已知AB=4,⊙O的半径为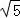 .
.
(1)分别求出线段AP、CB的长;
(2)如果OE=5,求证:DE是⊙O的切线;
(3)如果tan∠E= ,求DC的长
,求DC的长
. 
解答:
(1)解:∵AC为直径,
∴∠ABC=90°,
在Rt△ABC中,AC=2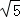 ,AB=4,
,AB=4,
∴BC=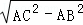 =2,--------------2分
=2,--------------2分
∵直径FG⊥AB,
∴AP=BP=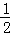 AB=2;--------------3分
AB=2;--------------3分
(2)证明:∵AP=BP,
∴OP为△ABC的中位线,
∴OP=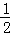 BC=1,
BC=1,
∴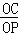 =
= ,
,
而 =
= =
=
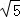 ,
,
∴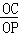 =
=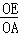 ,--------------5分
,--------------5分
∵∠EOC=∠AOP,
∴△EOC∽△AOP,--------------6分
∴∠OCE=∠OPA=90°,
∴OC⊥DE,
∴DE是⊙O的切线;--------------7分
(3)解:∵BC∥EP,
∴∠DCB=∠E,
∴tan∠DCB=tan∠E=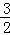
在Rt△BCD中,BC=2,tan∠DCB=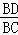 =
=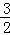 ,
,
∴BD=3,-------------9分
∴CD=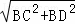 =
= ,--------------10分
,--------------10分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
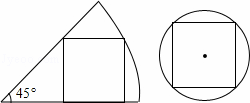
一张圆心角为45°的扇形纸板和圆形纸板按如图方式分别剪成一个正方形,边长都为1,则扇形和圆形纸板的面积比是--------( )
|
| A. | 5:4 | B. | 5:2 | C. |
| D. |
|
 :2
:2
 B.
B. C.
C. D.
D.
 ,则
,则 ( )
( )
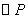 过点C,若C的坐标为(0,2),AB=5, 经过A、B、C三点的抛物线为y=ax2+bx+c。
过点C,若C的坐标为(0,2),AB=5, 经过A、B、C三点的抛物线为y=ax2+bx+c。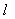 交x轴于点D,交圆于点E。
交x轴于点D,交圆于点E。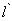 分别交射线CA,CB(点C除外)于点M,N,则
分别交射线CA,CB(点C除外)于点M,N,则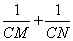 的值是否为定值,若是,求出定值,若不是,请说明理由
的值是否为定值,若是,求出定值,若不是,请说明理由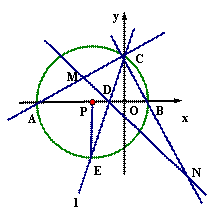
 的解集是___________.
的解集是___________.