题目内容
如图, 边长是5的正方形 内, 半径为2的⊙
内, 半径为2的⊙ 与边
与边 和
和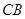
相切, ⊙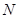 与⊙
与⊙ 外切于点
外切于点 , 并且
, 并且 与边
与边 和
和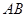 相切.
相切. 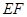 是两圆的内公切线, 点
是两圆的内公切线, 点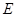 和
和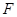 分别在
分别在 和
和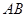 上. 则
上. 则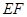 的长等于 _______ .
的长等于 _______ .
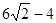
解析试题分析:由题意分析可知,设AB交圆N于点P,交AD于点Q
所以FP=EQ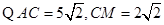
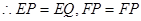
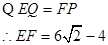
考点:圆和圆的位置关系
点评:圆与圆的位置关系判断条件,确定位置关系.设两圆的半径分别为R和r,且R≥r,圆心距为d:外离,则d>R+r;外切,则d=R+r;相交,则R-r<d<R+r;内切,则d=R-r;内含,则d<R-r.

练习册系列答案
相关题目

 25、如图,边长为3的正△ABC中,M、N分别位于AC、BC上,且AM=1,BN=2.过C、M、N三点的圆交△ABC的一条对称轴于另一点0.求证:点O是正△ABC的中心.
25、如图,边长为3的正△ABC中,M、N分别位于AC、BC上,且AM=1,BN=2.过C、M、N三点的圆交△ABC的一条对称轴于另一点0.求证:点O是正△ABC的中心. 如图,边长为1的正六边形纸片是轴对称图形,它的对称轴的条数是( )
如图,边长为1的正六边形纸片是轴对称图形,它的对称轴的条数是( )
