题目内容
 如图,在圆心角为120°的弧ACB的两端引相交于点D的两条切线,⊙O′与AD、BD、
如图,在圆心角为120°的弧ACB的两端引相交于点D的两条切线,⊙O′与AD、BD、 |
| ACB |
考点:切线的性质,弧长的计算
专题:
分析:连接O'E,设⊙O的半径是R,则弧ACB的长是:
=
,设⊙O'的半径是r,利用相切两圆的圆心距等于两圆的半径的和以及直角三角形的性质,利用R表示出r,求得⊙O′的周长,从而进行比较.
| 120πR |
| 180 |
| 2πR |
| 3 |
解答: 解:连接O'E,
解:连接O'E,
∵AD是圆的切线,
∴OA⊥AD,O'E⊥AD,
∴OA∥O'E.
设⊙O的半径是R,则弧ACB的长是:
=
,
设⊙O'的半径是r,
∵∠AOB=120°,
∴∠AOD=60°,∠EO'D=60°,
∴∠ODA=30°,
∴OD=2OA=2R,O'D=2O'D=2r,
又OO'=R+r,
∴R+r+2r=2R,
则r=
,
则较⊙O′的周长是2πr=
.
则⊙O′的周长与弧ACB的长相等.
 解:连接O'E,
解:连接O'E,∵AD是圆的切线,
∴OA⊥AD,O'E⊥AD,
∴OA∥O'E.
设⊙O的半径是R,则弧ACB的长是:
| 120πR |
| 180 |
| 2πR |
| 3 |
设⊙O'的半径是r,
∵∠AOB=120°,
∴∠AOD=60°,∠EO'D=60°,
∴∠ODA=30°,
∴OD=2OA=2R,O'D=2O'D=2r,
又OO'=R+r,
∴R+r+2r=2R,
则r=
| R |
| 3 |
则较⊙O′的周长是2πr=
| 2πR |
| 3 |
则⊙O′的周长与弧ACB的长相等.
点评:本题考查了切线的性质定理,以及相切的量圆的性质,利用R表示出r是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
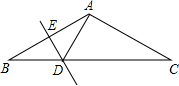 如图,AB=AC,∠BAC=120°,AB的垂直平分线交BC于点D,交AB于点E,则∠ADC的度数是( )
如图,AB=AC,∠BAC=120°,AB的垂直平分线交BC于点D,交AB于点E,则∠ADC的度数是( )| A、30° | B、60° |
| C、45° | D、65° |
 如图,在长方形的台球桌面上,选择适当的角度打击白球,可以使白球经过两次反弹后将黑球直接撞入袋中,此时∠1=∠2,∠3=∠4,并且∠2+∠3=90°,∠4+∠5=90°.如果黑球与洞口的连线和台球桌面边缘的夹角∠5=40°,那么∠1应该等于多少度才能保证黑球准确入袋?请说明理由.
如图,在长方形的台球桌面上,选择适当的角度打击白球,可以使白球经过两次反弹后将黑球直接撞入袋中,此时∠1=∠2,∠3=∠4,并且∠2+∠3=90°,∠4+∠5=90°.如果黑球与洞口的连线和台球桌面边缘的夹角∠5=40°,那么∠1应该等于多少度才能保证黑球准确入袋?请说明理由. 如图,点E是∠ABC的平分线与△ABC的外角∠ACD的平分线CE的交点,∠A=64°,你能求出∠E的度数吗?
如图,点E是∠ABC的平分线与△ABC的外角∠ACD的平分线CE的交点,∠A=64°,你能求出∠E的度数吗?