题目内容
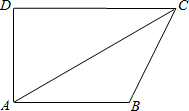（2013•攀枝花模拟）在四边形ABCD中，AB∥CD，∠D=90°，∠DCA=30°，CA平分∠DCB，AD=4cm，求AB的长度？
分析：过B作BE⊥AC，由AD=4m和∠D=90°，∠DCA=30°，可以求出AC的长，根据平行线的性质和角平分线以及等腰三角形的性质即可求出AD的长．
解答：解：∵∠D=90°，∠DCA=30°，AD=4cm，
∴AC=2AD=8cm，
∵CA平分∠DCB，AB∥CD，
∴∠CAB=∠ACB=30°，
∴AB=BC，
过B作BE⊥AC，
∴AE=
AC=4cm，
∴cos∠EAB=
=
，
∴AB=
cm．
∴AC=2AD=8cm，
∵CA平分∠DCB，AB∥CD，
∴∠CAB=∠ACB=30°，
∴AB=BC，
过B作BE⊥AC，
∴AE=
| 1 |
| 2 |
∴cos∠EAB=
| AE |
| AB |
| ||
| 2 |
∴AB=
8
| ||
| 3 |
点评：本题考查了平行线的性质、角平分线的定义以及等腰三角形的性质，解题的关键是作高线构造直角三角形，利用锐角三角函数求出AB的长．
练习册系列答案
相关题目
（2013•攀枝花模拟）如图，点G是△ABC的重心，CG的延长线交AB于D，GA=5，GC=4，GB=3，将△ADG绕点D顺时针方向旋转180°得到△BDE，则△EBC的面积=
