��Ŀ����
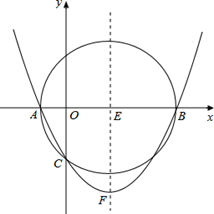
��ͼ����֪������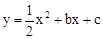 ��b��c�dz�������c<0����x��ֱ��ڵ�A��B����Aλ�ڵ�B����ࣩ����y��ĸ����ύ�ڵ�C����A������Ϊ(��1��0)��
��b��c�dz�������c<0����x��ֱ��ڵ�A��B����Aλ�ڵ�B����ࣩ����y��ĸ����ύ�ڵ�C����A������Ϊ(��1��0)��
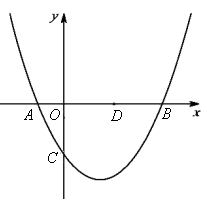
��1��b���� �� ����B�ĺ�����Ϊ�� �� ������������ú�c�Ĵ���ʽ��ʾ����
��2������BC������A��ֱ��AE��BC����������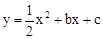 ���ڵ�E����D��x����һ�㣬������Ϊ
���ڵ�E����D��x����һ�㣬������Ϊ
(2��0)����C��D��E������ͬһֱ����ʱ���������ߵĽ���ʽ��
��3���ڣ�2���������£���P��x���·����������ϵ�һ���㣬����PB��PC�������á�PBC�����ΪS��
����S��ȡֵ��Χ��
������PBC�����SΪ�������������ġ�PBC������ �� ����
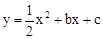 ��b��c�dz�������c<0����x��ֱ��ڵ�A��B����Aλ�ڵ�B����ࣩ����y��ĸ����ύ�ڵ�C����A������Ϊ(��1��0)��
��b��c�dz�������c<0����x��ֱ��ڵ�A��B����Aλ�ڵ�B����ࣩ����y��ĸ����ύ�ڵ�C����A������Ϊ(��1��0)��
��1��b���� �� ����B�ĺ�����Ϊ�� �� ������������ú�c�Ĵ���ʽ��ʾ����
��2������BC������A��ֱ��AE��BC����������
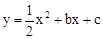 ���ڵ�E����D��x����һ�㣬������Ϊ
���ڵ�E����D��x����һ�㣬������Ϊ(2��0)����C��D��E������ͬһֱ����ʱ���������ߵĽ���ʽ��
��3���ڣ�2���������£���P��x���·����������ϵ�һ���㣬����PB��PC�������á�PBC�����ΪS��
����S��ȡֵ��Χ��
������PBC�����SΪ�������������ġ�PBC������ �� ����
�⣺��1�� ��
�� ��
��
��2����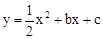 ����x=0����y=c��
����x=0����y=c��
���C��������c��0����
��ֱ��BC�Ľ���ʽΪ ��
��
�ߵ�B������Ϊ(��2 c��0)���� ��
��
�� ����
���� ��
��
��ֱ��BC�Ľ���ʽΪ ��
��
��AE��BC�������ֱ��AE�Ľ���ʽΪ ��
��
�ߵ�A������Ϊ(��1��0)���� ��
�� ��
��
��ֱ��AE�Ľ���ʽΪ ��
��
�� ���
��� ��
��
���E������Ϊ ��
��
�ߵ�C������Ϊ ����D������Ϊ��2��0������ֱ��CD�Ľ���ʽΪ
����D������Ϊ��2��0������ֱ��CD�Ľ���ʽΪ ��
��
�ߵ�C��D��E������ͬһֱ���ϣ��� ��
��
�� �����
����� ����ȥ����
����ȥ����
�� ��
��
�������ߵĽ���ʽΪ ��
��
��3�������P������Ϊ ��
��

�ߵ�A������Ϊ(��1��0)����B������Ϊ(4��0)����C������Ϊ��0����2����
��AB=5��OC=2��ֱ��CB�Ľ���ʽΪ ��
��
�� ʱ��
ʱ�� ��
��
�� ����
���� ��
��
�� ʱ������P��PG��x���ڵ�G����BC�ڵ�F��
ʱ������P��PG��x���ڵ�G����BC�ڵ�F��
���F������Ϊ ��
��
�� ��
��
�� ��
��
�൱x=2ʱ�� ����
���� ��
��
����������S��ȡֵ��ΧΪ ��
��
��11��
 ��
�� ��
����2����
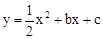 ����x=0����y=c��
�У���x=0����y=c�����C������Ϊ��c��0����
��ֱ��BC�Ľ���ʽΪ
 ��
���ߵ�B������Ϊ(��2 c��0)����
 ��
����
 ����
���� ��
����ֱ��BC�Ľ���ʽΪ
 ��
����AE��BC�������ֱ��AE�Ľ���ʽΪ
 ��
���ߵ�A������Ϊ(��1��0)����
 ��
�� ��
����ֱ��AE�Ľ���ʽΪ
 ��
����
 ���
��� ��
�����E������Ϊ
 ��
���ߵ�C������Ϊ
 ����D������Ϊ��2��0������ֱ��CD�Ľ���ʽΪ
����D������Ϊ��2��0������ֱ��CD�Ľ���ʽΪ ��
���ߵ�C��D��E������ͬһֱ���ϣ���
 ��
����
 �����
����� ����ȥ����
����ȥ������
 ��
���������ߵĽ���ʽΪ
 ��
����3�������P������Ϊ
 ��
��
�ߵ�A������Ϊ(��1��0)����B������Ϊ(4��0)����C������Ϊ��0����2����
��AB=5��OC=2��ֱ��CB�Ľ���ʽΪ
 ��
����
 ʱ��
ʱ�� ��
����
 ����
���� ��
����
 ʱ������P��PG��x���ڵ�G����BC�ڵ�F��
ʱ������P��PG��x���ڵ�G����BC�ڵ�F�����F������Ϊ
 ��
����
 ��
����
 ��
���൱x=2ʱ��
 ����
���� ��
������������S��ȡֵ��ΧΪ
 ��
����11��
�����������1������A������Ϊ(��1��0)����
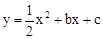 ��
�� ��
����
 ��
����
 �����
����� ��
�����B�ĺ�����Ϊ
 ��
����2�����ֱ��BC�Ľ���ʽ���Ӷ����ֱ��AE�Ľ���ʽ���õ���E������Ϊ
 ���ɵ�C��D��E������ͬһֱ���ϣ���
���ɵ�C��D��E������ͬһֱ���ϣ��� ����ֱ��CD�Ľ���ʽ
����ֱ��CD�Ľ���ʽ �������c���ɣ�1��
�������c���ɣ�1�� ���b���Ӷ��õ������ߵĽ���ʽ��
���b���Ӷ��õ������ߵĽ���ʽ����3���ٷ�
 ��
�� ����������ۡ�
����������ۡ��ڵ�
 ʱ��
ʱ�� ����SΪ��������Ӧ��x��4����
����SΪ��������Ӧ��x��4������
 ʱ��
ʱ�� ��
�� ����SΪ��������Ӧ��x��7����
����SΪ��������Ӧ��x��7���� ʱֻ��1������
ʱֻ��1������������PBC�����SΪ�������������ġ�PBC����11����

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ

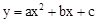 ������A��0��3����B��3��0����C��4��3����
������A��0��3����B��3��0����C��4��3����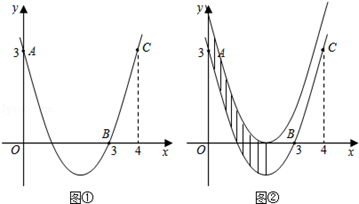
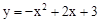 ��ͼ������ƽ��1����λ��������ƽ��2����λ����ƽ�ƺ�������ߵĽ���ʽ��ƽ�ƺ������ߵ���״���䣩��
��ͼ������ƽ��1����λ��������ƽ��2����λ����ƽ�ƺ�������ߵĽ���ʽ��ƽ�ƺ������ߵ���״���䣩��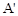 ��
��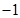 ��3����������ƽ��2����λ�õ�
��3����������ƽ��2����λ�õ�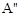 ��
��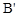 ��0��4����������ƽ��2����λ�õ�
��0��4����������ƽ��2����λ�õ� ��0��2����
��0��2����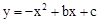 ��
��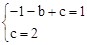 ����ã�
����ã�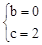 ��
�� ��
��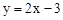 ����ƽ��3����λ��������ƽ��1����λ����ƽ�ƺ��ֱ�ߵĽ���ʽ��
����ƽ��3����λ��������ƽ��1����λ����ƽ�ƺ��ֱ�ߵĽ���ʽ��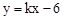 ��������
�������� �ཻ��A��B���㣬�ҵ�A��1����4��Ϊ�����ߵĶ��㣬��B��x���ϡ�
�ཻ��A��B���㣬�ҵ�A��1����4��Ϊ�����ߵĶ��㣬��B��x���ϡ�
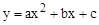 ����A��B��C���㣬����ΪF��
����A��B��C���㣬����ΪF��