题目内容
一次函数y=ax+b与反比例函数 ,x与y的对应值如表:
,x与y的对应值如表:
| x | -3 | -2 | -1 | 1 | 2 | 3 |
| y=ax+b | 4 | 3 | 2 | 0 | -1 | -2 |
 |  | 1 | 2 | -2 | -1 |  |
 的解为________;不等式ax+b>-
的解为________;不等式ax+b>- 的解集为________.
的解集为________.
-1、2 x<-1或0<x<2
分析:直接根据两函数的对应值表找出y的值对应相等的值即可求出方程ax+b=- 的解;再根据方程ax+b=-
的解;再根据方程ax+b=- 的解画出函数图象,利用数形结合求出等式ax+b>-
的解画出函数图象,利用数形结合求出等式ax+b>- 的解集即可.
的解集即可.
解答: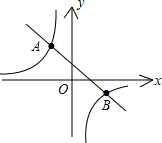 解:∵由x与y的对应值表可知,当x=-1或x=2时,两函数的值相等,
解:∵由x与y的对应值表可知,当x=-1或x=2时,两函数的值相等,
∴方程ax+b=- 的解为-1、2;
的解为-1、2;
设一次函数y=ax+b与反比例函数 的交点坐标为A、B,
的交点坐标为A、B,
∵当x=-1或x=2时,两函数的值相等,
∴A(-1,2),B(2,-1),
两函数的大致图象如图:
∵由两函数的图象可知,当x<-1或0<x<2一次函数的图象在反比例函数图象的上方,
∴不等式ax+b>- 的解集为:x<-1或0<x<2.
的解集为:x<-1或0<x<2.
故答案为:-1、2;x<-1或0<x<2.
点评:本题考查的是反比例函数与一次函数的交点问题,能根据所给的函数对应值表求出方程ax+b=- 的解是解答此题的关键.
的解是解答此题的关键.
分析:直接根据两函数的对应值表找出y的值对应相等的值即可求出方程ax+b=-
 的解;再根据方程ax+b=-
的解;再根据方程ax+b=- 的解画出函数图象,利用数形结合求出等式ax+b>-
的解画出函数图象,利用数形结合求出等式ax+b>- 的解集即可.
的解集即可.解答:
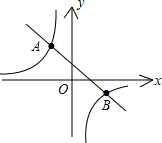 解:∵由x与y的对应值表可知,当x=-1或x=2时,两函数的值相等,
解:∵由x与y的对应值表可知,当x=-1或x=2时,两函数的值相等,∴方程ax+b=-
 的解为-1、2;
的解为-1、2;设一次函数y=ax+b与反比例函数
 的交点坐标为A、B,
的交点坐标为A、B,∵当x=-1或x=2时,两函数的值相等,
∴A(-1,2),B(2,-1),
两函数的大致图象如图:
∵由两函数的图象可知,当x<-1或0<x<2一次函数的图象在反比例函数图象的上方,
∴不等式ax+b>-
 的解集为:x<-1或0<x<2.
的解集为:x<-1或0<x<2.故答案为:-1、2;x<-1或0<x<2.
点评:本题考查的是反比例函数与一次函数的交点问题,能根据所给的函数对应值表求出方程ax+b=-
 的解是解答此题的关键.
的解是解答此题的关键. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
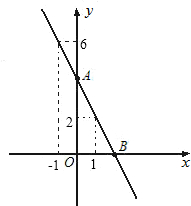 已知如图,一次函数y=ax+b图象经过点(1,2)、点(-1,6).求:
已知如图,一次函数y=ax+b图象经过点(1,2)、点(-1,6).求: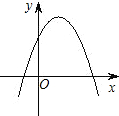 已知二次函数y=ax2+bx+c的图象如图所示,则在同一坐标系中,一次函数y=ax+c和反比例函数y=
已知二次函数y=ax2+bx+c的图象如图所示,则在同一坐标系中,一次函数y=ax+c和反比例函数y=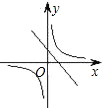
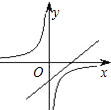
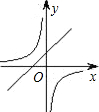
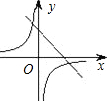
 如图,一次函数y=ax+b的图象与反比例函数y=
如图,一次函数y=ax+b的图象与反比例函数y=