题目内容
矩形ABCD的对角线交于O点,一条边的长为1,△AOB是正三角形,则这个矩形的周长为________.
2+2 或
或 +2
+2
分析:画出图形,根据矩形的对角线互相平分且相等可得AC=2OB,再根据等边三角形的三边都相等,然后求出AC=2AB,然后分①AB=1时,利用勾股定理列式求出BC,②BC=1时,利用勾股定理列式求出AB的长,再根据矩形的周长公式列式计算即可得解.
解答: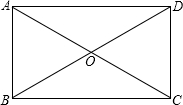 解:在矩形ABCD中,AC=2OB,
解:在矩形ABCD中,AC=2OB,
∵△AOB是正三角形,
∴OB=AB,
∴AC=2AB,
①AB=1时,AC=2,
根据勾股定理,BC= =
= =
= ,
,
所以,矩形的周长=2(AB+BC)=2(1+ )=2+2
)=2+2 ;
;
②BC=1时,根据勾股定理,AB2+BC2=AC2,
所以,AB2+12=(2AB)2,
解得AB= ,
,
所以,矩形的周长=2(AB+BC)=2( +1)=
+1)= +2;
+2;
综上所述,矩形的周长为2+2 或
或 +2.
+2.
故答案为:2+2 或
或 +2.
+2.
点评:本题考查了矩形的对角线互相平分且相等的性质,等边三角形的性质,难点在于要分情况讨论.
 或
或 +2
+2分析:画出图形,根据矩形的对角线互相平分且相等可得AC=2OB,再根据等边三角形的三边都相等,然后求出AC=2AB,然后分①AB=1时,利用勾股定理列式求出BC,②BC=1时,利用勾股定理列式求出AB的长,再根据矩形的周长公式列式计算即可得解.
解答:
 解:在矩形ABCD中,AC=2OB,
解:在矩形ABCD中,AC=2OB,∵△AOB是正三角形,
∴OB=AB,
∴AC=2AB,
①AB=1时,AC=2,
根据勾股定理,BC=
 =
= =
= ,
,所以,矩形的周长=2(AB+BC)=2(1+
 )=2+2
)=2+2 ;
;②BC=1时,根据勾股定理,AB2+BC2=AC2,
所以,AB2+12=(2AB)2,
解得AB=
 ,
,所以,矩形的周长=2(AB+BC)=2(
 +1)=
+1)= +2;
+2;综上所述,矩形的周长为2+2
 或
或 +2.
+2.故答案为:2+2
 或
或 +2.
+2.点评:本题考查了矩形的对角线互相平分且相等的性质,等边三角形的性质,难点在于要分情况讨论.

练习册系列答案
相关题目

 如图:矩形ABCD的对角线AC=10,BC=8,则图中五个小矩形的周长之和为
如图:矩形ABCD的对角线AC=10,BC=8,则图中五个小矩形的周长之和为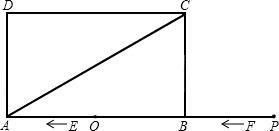 如图,矩形ABCD中,AB=6,BC=2
如图,矩形ABCD中,AB=6,BC=2 已知:如图,矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AB=5cm,则矩形对角线的长是
已知:如图,矩形ABCD的对角线AC、BD相交于点O,∠AOD=120°,AB=5cm,则矩形对角线的长是