Question

【题目】在中，是角平分线，．

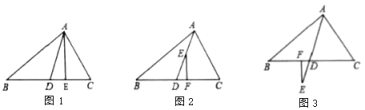
（1）如图1，是高，，，则 （直接写出结论，不需写解题过程）；

（2）如图2，点在上，于，试探究与、之间的数量关系，写出你的探究结论并证明；

（3）如图3，点在的延长线上，于，则与、之间的数量关系是 　（直接写出结论，不需证明）.

Answer 1

【答案】(1) 11；(2) ∠DEF=(∠C-∠B)，证明见解析；(3) ∠DEF=(∠C-∠B) ，证明见解析

【解析】

(1)依据角平分线的定义以及垂线的定义，即可得到∠CAD=∠BAC，∠CAE=90°-∠C，进而得出∠DAE=(∠C-∠B)，由此即可解决问题．
(2)过A作AG⊥BC于G，依据平行线的性质可得∠DAG=∠DEF，依据(1)中结论即可得到∠DEF=(∠C-∠B)．
(3)过A作AG⊥BC于G，依据平行线的性质可得∠DAG=∠DEF，依据(1)中结论即可得到∠DEF=(∠C-∠B)不变．

(1)∵AD平分∠BAC，
∴∠CAD=∠BAC，
∵AE⊥BC，
∴∠CAE=90°-∠C，
∴∠DAE=∠CAD-∠CAE
=∠BAC-(90°-∠C)
=(180°-∠B-∠C)-(90°-∠C)
=∠C-∠B
=(∠C-∠B)，
∵∠B=52°，∠C=74°，
∴∠DAE=(74°-52°)=11°；
(2)结论：∠DEF=(∠C-∠B)．
理由：如图2，过A作AG⊥BC于G，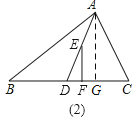

∵EF⊥BC，
∴AG∥EF，
∴∠DAG=∠DEF，
由(1)可得，∠DAG=(∠C-∠B)，
∴∠DEF=(∠C-∠B)；
(3)仍成立．
如图3，过A作AG⊥BC于G，

∵EF⊥BC，
∴AG∥EF，
∴∠DAG=∠DEF，
由(1)可得，∠DAG=(∠C-∠B)，
∴∠DEF=(∠C-∠B)，
故答案为∠DEF=(∠C-∠B)．