题目内容
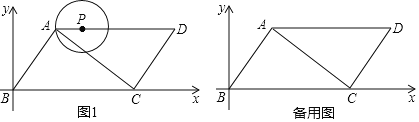
【题目】如图，已知
是
的直径，
，
是的弦，
交于点
，过点
作的切线交
的延长线于点
，连接
并延长交
的延长线于点
.
（1）求证：是的切线；
（2）若
，
，求线段
的长.
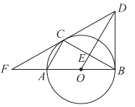
【答案】（1）见解析（2）8
【解析】
（1）连接OC，根据平行线的性质得到∠1=∠ACB，由圆周角定理得到∠1=∠ACB=90°，根据线段垂直平分线的性质得到DB=DC，求得∠DBE=∠DCE，根据切线的性质得到∠DBO=90°，求得OC⊥DC，于是得到结论；
（2）根据切线的性质得出
是等边三角形，再根据等边三角形的性质即可解答.
（1）证明：连接
∵
∴
∵
是
的直径
∴
∴
,由垂径定理得
垂直平分
.
∴
∴
又∵
∴
，即
∵
为的切线，
是半径
∴
∴
，即
，
∵是的半径.
∴
是的切线
（2）由（1）知是的切线
∴
在
中，
∴
又∵
∴是等边三角形
∴
∴
∴
练习册系列答案
相关题目
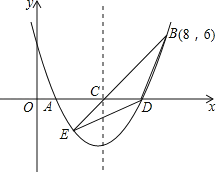
【题目】已知二次函数
的y与x的部分对应值如表：
x | 1 | 0 | 2 | 3 | 4 |
y | 5 | 0 | 4 | 3 | 0 |
下列结论：①抛物线的开口向上;②抛物线的对称轴为直线x=2;③当0<x<4时,y>0;④抛物线与x轴的两个交点间的距离是4;⑤若A(
,2),B(
,3)是抛物线上两点,则
,其中正确的个数是 ( )
A. 2B. 3C. 4D. 5
