题目内容
【题目】综合与实践
操作发现
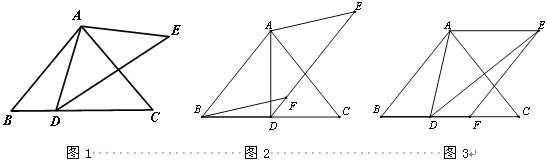
如图，在平面直角坐标系中，已知线段
两端点的坐标分别为
，
，点
的坐标为
，将线段沿
方向平移，平移的距离为的长度.
（1）画出平移后的线段
，直接写出点
对应点
的坐标；
（2）连接
，
，
，已知平分
，求证：
；
拓展探索
（3）若点
为线段上一动点（不含端点），连接
，
，试猜想
，
和
之间的关系，并说明理由.
【答案】（1）点
的坐标为
；（2）见解析；（3）
，理由见解析
【解析】
（1）按要求作出图形，并根据平移的性质写出点N的坐标即可；
（2）由平移的性质可得出
，
，再由平行的性质和角平分线的定义可得出
；
（3）过点
作
交
于点
，由平行的性质容易证明。
解：（1）所作线段如图所示.
点的坐标为.
（2）证明：根据平移的性质，可知，，.
∴
，
.
∵
平分
，
∴
.
∴.
（3）.
理由如下：
如图，过点作交于点，
又∵，
∴
.
∴
，
.
∴
.
练习册系列答案
相关题目
