题目内容
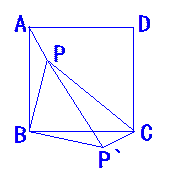
你还记得图形的旋转吗?如图,P是正方形ABCD内一点,PA=a,PB=2a,PC=3a.将△APB绕点B按顺时针方向旋转,使AB与BC重合,得△CBP,
1.求证:△PBP,是等腰直角三角形;
2.猜想△PCP,的形状,并说明理由.(考查逻辑推理能力)

【答案】
1.证明:由图形旋转可知: △APB≌△CP′B , ……………2分
∴BP=BP′=2a, AP=CP′=a.且∠ABP=∠CBP′………2分
由ABCD是正方形,得∠ABC=90°, ∴∠PBP′=90,∴△PBP′是等腰直角三角形。…4分
2.由(1)所证△PBP′是等腰直角三角形,
∴PP′= 
 ,
……………6分
,
……………6分
在△PP′C中,PP′= ,PC =
,PC =  ,CP′=
,CP′= 
且 ∴△PCP,是直角三角形…7分
∴△PCP,是直角三角形…7分
【解析】略

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
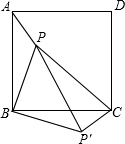 旋转,使AB和BC重合,得△CBP′.
旋转,使AB和BC重合,得△CBP′.