题目内容
【题目】如图，已知抛物线y=ax2+bx+c经过A（﹣2，0），B（4，0），C（0，3）三点．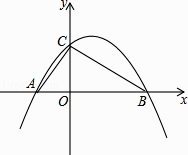
（1）求该抛物线的解析式；
（2）在y轴上是否存在点M，使△ACM为等腰三角形？若存在，请直接写出所有满足要求的点M的坐标；若不存在，请说明理由；
（3）若点P（t，0）为线段AB上一动点（不与A，B重合），过P作y轴的平行线，记该直线右侧与△ABC围成的图形面积为S，试确定S与t的函数关系式．
【答案】
（1）
解：把A（﹣2，0），B（4，0），C（0，3）代入抛物线y=ax2+bx+c得：
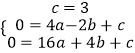，解得： 
，
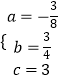则抛物线的解析式是：y=﹣ 
x2+ 
x+3
（2）
解：如图1，作线段CA的垂直平分线，交y轴于M，交AC与N，连结AM1，则△AM1C是等腰三角形，
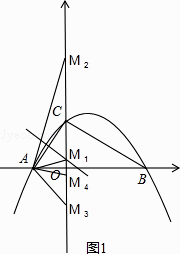
∵AC= 
= 
，
∴CN= 
，
∵△CNM1∽△COA，
∴ 
= 
，
∴ 
= 
，
∴CM1= 
，
∴OM1=OC﹣CM1=3﹣ = 
，
∴M1的坐标是（0， ），
当CA=CM2= 时，则△AM2C是等腰三角形，
则OM2=3+ ，
M2的坐标是（0，3+ ），
当CA=AM3= 时，则△AM3C是等腰三角形，
则OM3=3，
M3的坐标是（0，﹣3），
当CA=CM4= 时，则△AM4C是等腰三角形，
则OM4= ﹣3，
M4的坐标是（0，3﹣ ），
（3）
解：如图2，当点P在y轴或y轴右侧时，
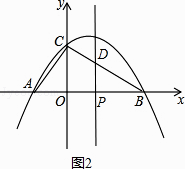
设直线与BC交于点D，
∵OB=4，OC=3，
∴S△BOC=6，
∵BP=BO﹣OP=4﹣t，
∴ 
= 
，
∵△BPD∽△BOC，
∴ 
=（ ）2，
∴ 
=（ ）2，
∴S=S△BPD= t2﹣3t+6（0≤t＜4）；
当点P在y轴左侧时，
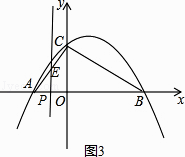
设直线与AC交与点E，
∵OP=﹣t，AP=t+2，
∴ 
= 
，
∵ 
=（ ）2，
∴ 
=（ ）2，
∴S△APE= 
，
∴S=S△ABC﹣S△APE=9﹣ =﹣ t2﹣3t+6（﹣2＜t＜0）．
【解析】（1）把A（﹣2，0），B（4，0），C（0，3）代入抛物线y=ax2+bx+c，求解即可；（2）作线段CA的垂直平分线，交y轴于M，交AC与N，连结AM1 ， 则△AM1C是等腰三角形，然后求出OM1得出M1的坐标，当CA=CM2时，则△AM2C是等腰三角形，求出OM2得出M2的坐标，当CA=AM3时，则△AM3C是等腰三角形，求出OM3得出M3的坐标，当CA=CM4时，则△AM4C是等腰三角形，求出OM4得出M4的坐标，（3）当点P在y轴或y轴右侧时，设直线与BC交与点D，先求出S△BOC ， 再根据△BPD∽△BOC，得出 =（ ）2 ， =（ ）2 ， 求出S=S△BPD；当点P在y轴左侧时，设直线与AC交与点E，根据 =（ ）2 ， 得出 =（ ）2 ， 求出S=S△ABC﹣S△APE=9﹣ ，再整理即可．
