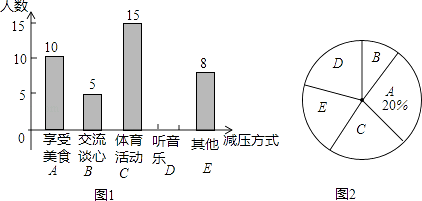
题目内容
【题目】先阅读下列解题过程,然后回答问题:
解方程: ![]()
解:①当![]() ≥0时,原方程可化为:
≥0时,原方程可化为: ![]() ,解得
,解得![]() ;
;
②当![]() <0时,原方程可化为:
<0时,原方程可化为: ![]() ,解得
,解得![]() ;
;
所以原方程的解是![]() 或
或![]()
(1)解方程: ![]()
(2)探究:当![]() 为何值时,方程
为何值时,方程![]() ①无解;②只有一个解;③有两个解。
①无解;②只有一个解;③有两个解。
【答案】(1)![]() 或
或![]() (2)
(2)![]() <
<![]() 时,方程
时,方程![]() 无解;
无解; ![]() =
=![]() 时,方程只有一个解;即
时,方程只有一个解;即![]() >
>![]() 时,方程
时,方程![]() 有两个解
有两个解
【解析】试题分析:(1)首先要认真审题,解此题时要理解绝对值的意义,要会去绝对值,然后化为一元一次方程即可求得.
(2)运用分类讨论进行解答.
试题解析:(1)当3x-2≥0时,原方程可化为:3x-2=4,
解得x=2;
当3x-2<0时,原方程可化为:3x-2=-4,
解得x=-![]() .
.
所以原方程的解是x=2或x=-![]() ;
;
(2)∵|x-2|≥0,
∴当b+1<0,即b<-1时,方程无解;
当b+1=0,即b=-1时,方程只有一个解;
当b+1>0,即b>-1时,方程有两个解.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目