题目内容
【题目】定义:有三个角相等的四边形叫做三等角四边形.
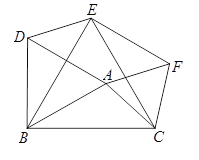
(1)在三等角四边形![]() 中,
中,![]() ,则
,则![]() 的取值范围为________.
的取值范围为________.
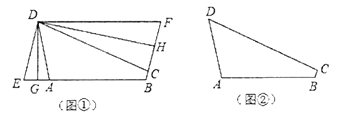
(2)如图①,折叠平行四边形![]() ,使得顶点
,使得顶点![]() 、
、![]() 分别落在边
分别落在边![]() 、
、![]() 上的点
上的点![]() 、
、![]() 处,折痕为
处,折痕为![]() 、
、![]() .求证:四边形
.求证:四边形![]() 为三等角四边形;
为三等角四边形;
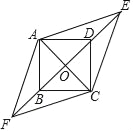
(3)如图②,三等角四边形![]() 中,
中,![]() ,若
,若![]() ,
,![]() ,
,![]() ,则
,则![]() 的长度为多少?
的长度为多少?
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() 的长度为
的长度为![]() .
.
【解析】
(1)根据四边形的内角和是360°,确定出∠BAD的范围;
(2)由四边形DEBF为平行四边形,得到∠E=∠F,且∠E+∠EBF=180°,再根据等角的补角相等,判断出∠DAB=∠DCB=∠ABC即可;
(3)延长BA,过D点作DG⊥BA,继续延长BA,使得AG=EG,连接DE;延长BC,过D点作DH⊥BC,继续延长BC,使得CH=HF,连接DF,由SAS证明△DEG≌△DAG,得出AD=DE=![]() ,∠DAG=∠DEA,由SAS证明△DFH≌△DCH,得出CD=DF=6,∠DCH=∠DFH,证出DE∥BF,BE∥DF,得出四边形DEBF是平行四边形,得出DF=BE=6,DE=BF=
,∠DAG=∠DEA,由SAS证明△DFH≌△DCH,得出CD=DF=6,∠DCH=∠DFH,证出DE∥BF,BE∥DF,得出四边形DEBF是平行四边形,得出DF=BE=6,DE=BF=![]() ,由等腰三角形的性质得出EG=AG=
,由等腰三角形的性质得出EG=AG=![]() (BE-AB)=1,在Rt△DGA中,由勾股定理求出DG=
(BE-AB)=1,在Rt△DGA中,由勾股定理求出DG=![]() =4,由平行四边形DEBF的面积求出
=4,由平行四边形DEBF的面积求出![]() ,在Rt△DCH中,由勾股定理求出
,在Rt△DCH中,由勾股定理求出![]() ,即可得出BC的长度.
,即可得出BC的长度.
(1)∵![]()
∴![]()
∴![]()
∵![]()
∴![]()
∴![]()
故答案为:![]()
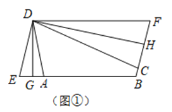
(2)证明:∵四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,
,![]()
∴![]()
∵![]() ,
,![]()
∴![]()
∵![]() ,
,![]() ,
,![]()
∴![]()
∴四边形![]() 是三等角四边形;
是三等角四边形;
(3)延长![]() ,过
,过![]() 点作
点作![]() ,继续延长
,继续延长![]() ,使得
,使得![]() ,连接
,连接![]() ;延长
;延长![]() ,过
,过![]() 点作
点作![]() ,继续延长
,继续延长![]() ,使得
,使得![]() ,连接
,连接![]() ,如图所示:
,如图所示:
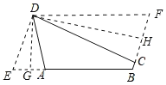
在![]() 和
和![]() 中,
中,
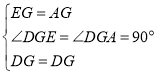
∴![]()
![]() ,
,
∴![]() ,
,![]()
同理可得![]() ,
,![]()
∴![]() ,
,![]()
∵![]()
∴![]() ,
,![]()
∴![]() ,
,![]()
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,![]() ,
,
∴![]()
在![]() 中,
中,![]()
∵平行四边形![]() 的面积
的面积![]() ,
,
即:![]()
∴![]()
在![]() 中,
中,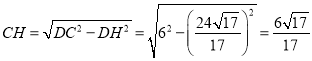
∴![]()
故答案为:![]() 的长度为
的长度为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】用同样规格的黑白两种颜色的正方形瓷砖,按下图的方式铺地板:

(1)观察图形,填写下表:
图形 | (1) | (2) | (3) | …… |
黑色瓷砖的块数 | 4 | …… | ||
黑白两种瓷砖的总块数 | 15 | …… |
(2)依上推测,第n个图形中黑色瓷砖的块数为__________________;黑白两种瓷砖的总块数为__________________(都用含n的代数式表示)
(3)白色瓷砖的块数可能比黑色瓷砖的块数多2014块吗?若能,求出是第几个图形;若不能,请说明理由.