题目内容
在正方形ABCD的边BC的延长线上取一点E，使EC=AC，连接AE交CD于F，那么∠AFC等于________°；若AB=2，那么△ACE的面积为________．
112.5 
分析：可由AC=CE求出∠E的大小，进而求出∠AFC，三角形的面积，用面积公式求出底边与高代入即可．
解答：
解：如图所示，
∵AC=CE，
∴∠CAE=∠E，
∵∠CAE+∠E=∠ACB=45°，
∴∠E=22.5°，
∴∠CFE=67.5°，
∴∠AFC=180°-∠CFE=180°-67.5°=112.5°，
∵AB=2，
∴CE=AC=2
，
∴SACE=
CE•AB=
×2×2=2．
故答案为：112.5°，2．
点评：熟练掌握正方形的性质，会利用其性质求解一些简单的计算问题．
分析：可由AC=CE求出∠E的大小，进而求出∠AFC，三角形的面积，用面积公式求出底边与高代入即可．
解答：
解：如图所示，∵AC=CE，
∴∠CAE=∠E，
∵∠CAE+∠E=∠ACB=45°，
∴∠E=22.5°，
∴∠CFE=67.5°，
∴∠AFC=180°-∠CFE=180°-67.5°=112.5°，
∵AB=2，
∴CE=AC=2
，∴SACE=
CE•AB=×2×2=2．故答案为：112.5°，2
．点评：熟练掌握正方形的性质，会利用其性质求解一些简单的计算问题．
练习册系列答案
阅读快车系列答案
相关题目
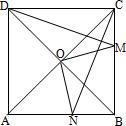42、如图，在正方形ABCD的边BC上任取一点M，过点C作CN⊥DM交AB于N，设正方形对角线交点为O，试确定OM与ON之间的关系，并说明理由．
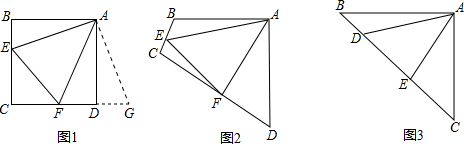
如图，正方形CEFG的对角线CF在正方形ABCD的边BC的延长线上（CE＞BC），点M在CF上，且MF=AB，线段AF与DM交于点N．