题目内容
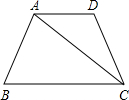
如图所示，在梯形ABCD中，AD∥BC，AB=CD，△ADE是等边三角形．若∠BAD=60°，AB=2a，BC=3a，则梯形中位线的长为________．
4a
分析：作辅助线，求出上底和下底的长，然后再利用梯形中位线定理求解．
解答：
解：如图：过B，C两点分别向AD作垂线，垂足分别为F、G，
∵在Rt△ABF中，AB=2a，∠BAD=60°，
∴∠ABF=30°，
∴AF=
AB=a，
同理可得DG=a，FG=BC=3a，
∴梯形中位线的长为：
=
=4a．
点评：此题考查的是梯形的中位线定理，解答此题的关键是去掉图中无关信息，再解直角三角形．
分析：作辅助线，求出上底和下底的长，然后再利用梯形中位线定理求解．
解答：
解：如图：过B，C两点分别向AD作垂线，垂足分别为F、G，∵在Rt△ABF中，AB=2a，∠BAD=60°，
∴∠ABF=30°，
∴AF=
AB=a，同理可得DG=a，FG=BC=3a，
∴梯形中位线的长为：
==4a．点评：此题考查的是梯形的中位线定理，解答此题的关键是去掉图中无关信息，再解直角三角形．
练习册系列答案
寒假天地重庆出版社系列答案
相关题目
已知如图所示，在梯形ABCD中，AD∥BC，AB=AD=DC=8，∠B=60°，连接AC．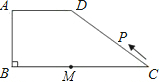
如图所示，在梯形ABCD中，AD∥BC，∠ABC=90°，AD=AB=6，BC=14，点M是线段BC上一定点，且MC=8．动点P从C点出发沿C?D?A?B的路线运动，运动到点B停止．在点P的运动过程中，使△PMC为等腰三角形的点P有
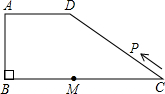如图所示，在梯形ABCD中，AD∥BC，∠ABC=90°，AD=AB=6，BC=14，点M是线段BC上一定点，且MC=8．动点P从C点出发沿C→D→A→B的路线运动，运动到点B停止．在点P的运动过程中，使△PMC为等腰三角形的点P有几个？并求出相应等腰三角形的腰长．
如图所示，在梯形ABCD中，已知AB∥CD，AD⊥DB，AD=DC=CB，AB=4，DO垂直于AB．则腰长是
如图所示，在梯形ABCD中，AB∥DC，EF是梯形的中位线，AC交EF于G，BD交EF于H，以下说法错误的是（ ）