题目内容
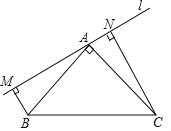
【题目】等腰直角△ABC,其中AB=AC,∠BAC=90°,过B、C作经过A点直线L的垂线,垂足分别为M、N
(1)你能找到一对三角形的全等吗?并说明理由.
(2)BM,CN,MN之间有何关系?
【答案】(1)△BMA≌△ANC,理由见解析;(2)MN=CN+BM.
【解析】
(1)根据题意证明∠MBA=∠NAC,利用AAS定理证明△ABM≌△CAN;
(2)根据全等三角形的性质得到CN=AM,BM=AN,结合图形解答.
(1)△BMA≌△ANC,
∵BM⊥MA,CN⊥AN,
∴∠BAC=∠BMA=∠CNA=90°,
∴∠MAB+∠CAN=90°,∠MBA+∠MAB=90°,
∴∠CAN=∠MBA,
在△ABM和△CAN中,
∵
∴△BMA≌△ANC(AAS).
(2)MN=CN+BM
理由是:∵△BMA≌△ANC.
∴MA=NC,BM=AN.
∵MN=AM+AN,
∴MN=CN+BM.

练习册系列答案
相关题目