Question

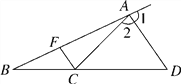
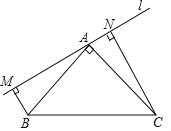
【题目】如图，已知△ABC中，∠ABC=90°，AB=BC，过△ABC的顶点B作直线，且点A到的距离为2，点C到的距离为3，则AC的长是（ ）

A. B. C. D. 5

Answer 1

【答案】C

【解析】

分别过A、C作AD⊥l于D，CE⊥l于E，根据锐角互余可得∠ABD=∠BCE，∠DAB=∠CBE，利用ASA可证明△ABD≌△CBE，即可得BD=CE，根据勾股定理可求出AB的长，再利用勾股定理求出AC的长即可.

分别过A、C作AD⊥l于D，CE⊥l于E，

∵点A到的距离为2，点C到的距离为3，

∴AD=2，CE=3，

∵∠ABD+∠BAD=90°，∠ABD+∠CBE=90°，

∴∠BAD=∠CBE，

同理：∠ABD=∠BCE，

∵∠ABD=∠BCE，AB=BC，∠BAD=∠CBE，

∴△ABD≌△CBE，

∴BD=CE=3，

在Rt△ABD中，AB2=22+32=13，

在Rt△ABC中，AC2=AB2+BC2=13+13=26，

∴AC=，

故选C.