题目内容
 如图,在直角三角形ABC中,∠ACB=90°,AD平分∠BAC交BC于D,E是AB上的一点,且BE=BC,CE交AD于一点P,求∠CPD的度数.
如图,在直角三角形ABC中,∠ACB=90°,AD平分∠BAC交BC于D,E是AB上的一点,且BE=BC,CE交AD于一点P,求∠CPD的度数.
解:如图,
∵∠ACB=90°,
∴∠ACE+∠BCE=90°,
又∵AD平分∠BAC,
∴∠CAD=∠DAB,
∵BE=BC,
∵∠ECB=∠CEB,
∴∠CEB=∠CAE+∠ACE=∠ECB,
∴∠ACB=∠ACE+∠CAE+∠ACE=2∠ACE+2∠CAD=90°,
∴∠CAD+∠ACE=45°,
∴∠CPD=∠CAD+∠ACE=45°.
分析:由在直角三角形ABC中,∠ACB=90°,可得∠ACE+∠BCE=90°,又由AD平分∠BAC,BE=BC,可得∠CEB=∠CAE+∠ACE=∠ECB,则可求得∠CAD+∠ACE=45°,继而求得答案.
点评:此题考查了等腰三角形的性质、角平分线的定义以及直角三角形的性质.此题难度适中,注意掌握数形结合思想的应用.
∵∠ACB=90°,
∴∠ACE+∠BCE=90°,
又∵AD平分∠BAC,
∴∠CAD=∠DAB,
∵BE=BC,
∵∠ECB=∠CEB,
∴∠CEB=∠CAE+∠ACE=∠ECB,
∴∠ACB=∠ACE+∠CAE+∠ACE=2∠ACE+2∠CAD=90°,
∴∠CAD+∠ACE=45°,
∴∠CPD=∠CAD+∠ACE=45°.
分析:由在直角三角形ABC中,∠ACB=90°,可得∠ACE+∠BCE=90°,又由AD平分∠BAC,BE=BC,可得∠CEB=∠CAE+∠ACE=∠ECB,则可求得∠CAD+∠ACE=45°,继而求得答案.
点评:此题考查了等腰三角形的性质、角平分线的定义以及直角三角形的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
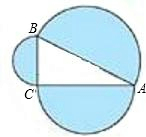 如图,在直角三角形ABC中,∠C=90°,AB=4,阴影部分的面积为( )
如图,在直角三角形ABC中,∠C=90°,AB=4,阴影部分的面积为( )| A、2π | B、3π | C、4π | D、6π |
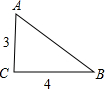
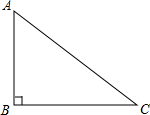 如图,在直角三角形中,一直角边比另一直角边长1,且斜边长为5.
如图,在直角三角形中,一直角边比另一直角边长1,且斜边长为5.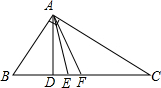 如图,在直角三角形ABC中,AD为斜边上的垂线,AE为角平分线,AF为中线,
如图,在直角三角形ABC中,AD为斜边上的垂线,AE为角平分线,AF为中线, 9、如图,在直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,则当AP=
9、如图,在直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,则当AP=