题目内容
如图，已知在Rt△ABC中，∠BAC=90°，AB=AC，M是AC的中点，AD⊥BM于E，交BC于D点．（1）求证：BD=2CD；
（2）若AM=
| 1 | n |
分析：作CG⊥AC交AD的延长线于G，易证△ABE≌△CAG得到AM=CG，△EBD∽△GCD，因而求
的值的问题可以转化为求
，根据相似三角形的性质就可求解．
| BD |
| CD |
| BE |
| CG |
解答：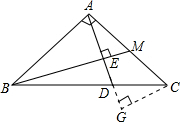
解：①作CG⊥AD交AD的延长线于G，证△ABE≌△CAG．
∴AE=CG，易证△ABM∽△EBA，则EB：AE=AB：AM=2：1，
∴△EBD∽△GCD，
∴BD：DC=EB：CG=EB：AE=2：1，
∴BD=2CD．
②作CG⊥AD交AD的延长线于G，易证△ABE≌△CAG，
∴AE=CG，设等腰直角三角形ABC的边AB=AC=2a，则AM=MC=a．
在Rt△ABM中，根据勾股定理得到BM=
a，AE=CG=
=
a，
∵BM⊥AD，CG⊥AD，
∴△AEM∽△AGC．
∴
=
=
，则EM=
•CG=
•
a，
∴BE=BM-EM=
a-
•
a=
a，
∴
=
=
．
解：①作CG⊥AD交AD的延长线于G，证△ABE≌△CAG．∴AE=CG，易证△ABM∽△EBA，则EB：AE=AB：AM=2：1，
∴△EBD∽△GCD，
∴BD：DC=EB：CG=EB：AE=2：1，
∴BD=2CD．
②作CG⊥AD交AD的延长线于G，易证△ABE≌△CAG，
∴AE=CG，设等腰直角三角形ABC的边AB=AC=2a，则AM=MC=a．
在Rt△ABM中，根据勾股定理得到BM=
| 5 |
| AB•AM |
| BM |
2
| ||
| 5 |
∵BM⊥AD，CG⊥AD，
∴△AEM∽△AGC．
∴
| EM |
| CG |
| AM |
| AC |
| 1 |
| n |
| 1 |
| n |
| 1 |
| n |
2
| ||
| 5 |
∴BE=BM-EM=
| 5 |
| 1 |
| n |
2
| ||
| 5 |
| 5n-2 |
| 5n |
| 5 |
∴
| BD |
| DC |
| BE |
| GC |
| 5n-2 |
| 2n |
点评：解决本题的关键是根据相似三角形的性质转化为另外两个线段的比的问题．
练习册系列答案
相关题目
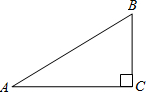如图，已知在Rt△ABC中，∠C=90°，BC=1，AC=2，则tanA的值为（ ）| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
（2012•驿城区模拟）如图，已知在Rt△ABC中，∠B=90°，D、E分别是边AB、AC的中点，若DE=4，AC=10，则AB的值为（ ）
如图，已知在Rt△ABC中，∠C=90°，内切圆的半径为3cm，外接圆的半径为12.5cm，求△ABC的三边长．
如图，已知在Rt△ABC中，∠C=90°，点D在BC上，AD=BD，sin∠ADC=
如图，已知在Rt△ABC中，∠C=90°．根据要求用尺规作图：