题目内容
如图，AB、AC是⊙O的两条切线，B、C是切点，若∠A=70°，则∠BOC的度数为
- A.130°
- B.120°
- C.110°
- D.100°
C
分析：利用切线的性质可得，∠B=∠C=90°，再用四边形的内角和为360度可解．
解答：∵AB、AC是⊙O的两条切线，B、C是切点，
∴∠B=∠C=90°，∠BOC=180°-∠A=110°．
故选C．
点评：本题利用了切线的性质，四边形的内角和为360度求解．
分析：利用切线的性质可得，∠B=∠C=90°，再用四边形的内角和为360度可解．
解答：∵AB、AC是⊙O的两条切线，B、C是切点，
∴∠B=∠C=90°，∠BOC=180°-∠A=110°．
故选C．
点评：本题利用了切线的性质，四边形的内角和为360度求解．
练习册系列答案
相关题目
D交OB的延长线于点D．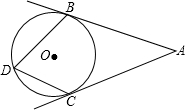
如图，AB、AC是⊙O的切线，且∠A=54°，则∠BDC=
如图，AB，AC是圆的两条弦，AD是圆的一条直径，且BC⊥AD，下列结论中不一定正确的是（ ）
如图，AB和AC是等腰△ABC的两腰，CD和BE是两腰上的高，CD和BE相交于点F．