题目内容
已知,Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,则△ABC的外接圆半径和△ABC的外心与内心之间的距离分别为
- A.5和

- B.
 和
和
- C.
 和
和
- D.
 和
和
B
分析:首先运用勾股定理求出斜边AB=5cm,因为直角三角形的外心是斜边的中点,则外接圆的半径是斜边的一半,即为 cm.直角三角形的内切圆的半径r和三边的关系为r=
cm.直角三角形的内切圆的半径r和三边的关系为r= (a,b为两直角边,c为斜边)可求的r.再运用勾股定理求外心与内心之间的距离即可.
(a,b为两直角边,c为斜边)可求的r.再运用勾股定理求外心与内心之间的距离即可.
解答: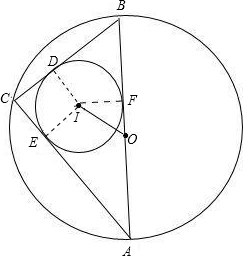 解:(1)∵∠C=90°,AC=3cm,BC=4cm,
解:(1)∵∠C=90°,AC=3cm,BC=4cm,
∴AB=5cm(勾股定理).
∴△ABC的外接圆半径长R= =
= cm;
cm;
(2)连接ID,IE,IF,
∵⊙I是△ABC的内切圆,
∴ID⊥BC,IE⊥AC,IF⊥AB,
∴∠CDI=∠CEI=∠C=90°,
又∵DI=EI,
∴四边形CDIE是正方形.
∴CD=CE=DI=IE;
∵AC=3cm,BC=4cm,由(1)知AB=5cm,
∴△ABC的内切圆半径长r= ,
,
=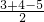
=1cm.
即DI=EI=FI=1cm;
∴CD=1cm.
∵BC=4cm,
∴BD=3cm.
∵⊙I是△ABC的内切圆,
∴BD=BF=3cm.
∵BO= cm,
cm,
∴OF= cm.
cm.
在Rt△IFO中,IO= cm(勾股定理).
cm(勾股定理).
∴△ABC的外心与内心之间的距离为 cm.
cm.
故选C.
点评:本题考查了三角形的外心和内心的性质.直角三角形的外心是斜边的中点,外接圆的半径是斜边的一半;直角三角形的内切圆的半径r和三边的关系为r= (a,b为两直角边,c为斜边).
(a,b为两直角边,c为斜边).
分析:首先运用勾股定理求出斜边AB=5cm,因为直角三角形的外心是斜边的中点,则外接圆的半径是斜边的一半,即为
 cm.直角三角形的内切圆的半径r和三边的关系为r=
cm.直角三角形的内切圆的半径r和三边的关系为r= (a,b为两直角边,c为斜边)可求的r.再运用勾股定理求外心与内心之间的距离即可.
(a,b为两直角边,c为斜边)可求的r.再运用勾股定理求外心与内心之间的距离即可.解答:
 解:(1)∵∠C=90°,AC=3cm,BC=4cm,
解:(1)∵∠C=90°,AC=3cm,BC=4cm,∴AB=5cm(勾股定理).
∴△ABC的外接圆半径长R=
 =
= cm;
cm;(2)连接ID,IE,IF,
∵⊙I是△ABC的内切圆,
∴ID⊥BC,IE⊥AC,IF⊥AB,
∴∠CDI=∠CEI=∠C=90°,
又∵DI=EI,
∴四边形CDIE是正方形.
∴CD=CE=DI=IE;
∵AC=3cm,BC=4cm,由(1)知AB=5cm,
∴△ABC的内切圆半径长r=
 ,
,=
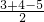
=1cm.
即DI=EI=FI=1cm;
∴CD=1cm.
∵BC=4cm,
∴BD=3cm.
∵⊙I是△ABC的内切圆,
∴BD=BF=3cm.
∵BO=
 cm,
cm,∴OF=
 cm.
cm.在Rt△IFO中,IO=
 cm(勾股定理).
cm(勾股定理).∴△ABC的外心与内心之间的距离为
 cm.
cm.故选C.
点评:本题考查了三角形的外心和内心的性质.直角三角形的外心是斜边的中点,外接圆的半径是斜边的一半;直角三角形的内切圆的半径r和三边的关系为r=
 (a,b为两直角边,c为斜边).
(a,b为两直角边,c为斜边). 
练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
已知在Rt△ABC中,∠C=90°,sinA
,则tanB的值为( )
| ||
| 2 |
| A、1 | ||||
B、
| ||||
C、
| ||||
D、
|
 如图,已知在Rt△ABC中,∠ACB=90°,AB=4,分别以AC、BC为直径作半圆,面积分别记为S1、S2,则S1+S2等于
如图,已知在Rt△ABC中,∠ACB=90°,AB=4,分别以AC、BC为直径作半圆,面积分别记为S1、S2,则S1+S2等于 如图,已知在Rt△ABC中,∠BAC=90°,AB=AC,M是AC的中点,AD⊥BM于E,交BC于D点.
如图,已知在Rt△ABC中,∠BAC=90°,AB=AC,M是AC的中点,AD⊥BM于E,交BC于D点. 如图:已知在Rt△ABC中,∠C=90°,AC=4,BC=3,在直线AC上找点P,使△ABP是等腰三角形,则AP的长度为
如图:已知在Rt△ABC中,∠C=90°,AC=4,BC=3,在直线AC上找点P,使△ABP是等腰三角形,则AP的长度为