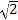题目内容
【题目】已知![]() 中,
中,![]() ,
,![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上(不与端点重合),
上(不与端点重合),![]() ,射线
,射线![]() 交
交![]() 延长线于点
延长线于点![]() ,点
,点![]() 在直线
在直线![]() 上,
上,![]() .
.
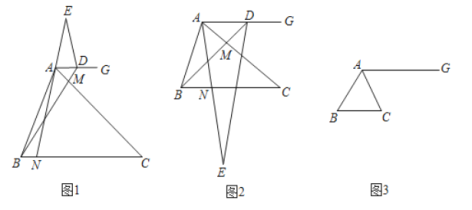
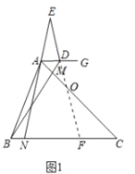
(1)(观察猜想)如图1,点![]() 在射线
在射线![]() 上,当
上,当![]() 时,
时,
①线段![]() 与
与![]() 的数量关系是______;
的数量关系是______;
②![]() 的度数是______;
的度数是______;
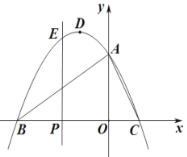
(2)(探究证明)如图2点![]() 在射线
在射线![]() 上,当
上,当![]() 时,判断并证明线段
时,判断并证明线段![]() 与
与![]() 的数量关系,求
的数量关系,求![]() 的度数;
的度数;
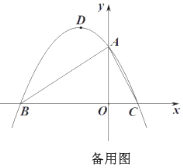
(3)(拓展延伸)如图3,点![]() 在直线
在直线![]() 上,当
上,当![]() 时,
时,![]() ,点
,点![]() 是
是![]() 边上的三等分点,直线
边上的三等分点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,请直接写出线段
,请直接写出线段![]() 的长.
的长.
【答案】(1)①![]() ,②
,②![]() ;(2)
;(2)![]() ;(3)满足条件的
;(3)满足条件的![]() 的长为
的长为![]() 或4.
或4.
【解析】
(1)①延长![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点O,先由等边对等角得到
于点O,先由等边对等角得到![]() ,然后证明
,然后证明![]() ,即可得到BM=AN;②再由等边对等角和平行线推出
,即可得到BM=AN;②再由等边对等角和平行线推出![]() ,由三角形外角性质得到
,由三角形外角性质得到![]() ,可推出
,可推出![]() ,即可得
,即可得![]() .
.
(2)同理可证![]() ,同(1)可推出
,同(1)可推出 ![]() ,最后得到
,最后得到![]() .
.
(3)当![]() 时,作
时,作![]() 于
于![]() ,在
,在![]() 中,利用60°可求出边长,然后在在
中,利用60°可求出边长,然后在在![]() 中求出BM,再由
中求出BM,再由![]() ,利用相似比求出CF,当
,利用相似比求出CF,当![]() 时,同法可求
时,同法可求![]() .
.
(1)①如图1中,延长![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点O.
于点O.
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;
②∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∵∠ANB+∠ENF=180°,∠BMA+∠BMC=180°,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
故答案为①![]() ,②
,②![]() .
.
(2)如图2中,设![]() 交
交![]() 于点
于点![]() .
.
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.

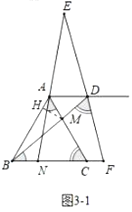
(3)①如图3-1中,当![]() 时,作
时,作![]() 于
于![]() .
.
由题意![]() ,在
,在![]() 中,
中,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
在![]() 中,
中,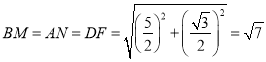 ,
,
由(2)可知:![]() ,∵
,∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
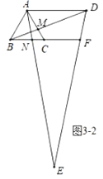
②如图3-2中,当![]() 时,同法可得
时,同法可得![]() .
.
综上所述,满足条件的![]() 的长为
的长为![]() 或4.
或4.

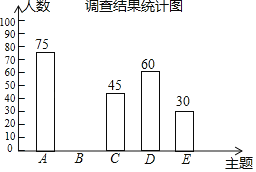
【题目】2019年3月19日,河南省教育厅发布《关于推进中小学生研学旅行的实施方案》,某中学为落实方案,给学生提供了以下五种主题式研学线路:A.“红色河南”,B.“厚重河南”C.“出彩河南”,D.“生态河南”,E.“老家河南”为了解学生最喜欢哪一种研学线路(每人只选取一种),随机抽取了部分学生进行调查,将调查结果绘制成如下不完整的统计表和统计图.根据以上信息解答下列问题:
调查结果统计表
主题 | 人数/人 | 百分比 |
A | 75 | n% |
B | m | 30% |
C | 45 | 15% |
D | 60 | |
E | 30 |
(1)本次接受调查的总人数为 人,统计表中m= ,n= .
(2)补全条形统计图.
(3)若把条形统计图改为扇形统计图,则“生态河南”主题线路所在扇形的圆心角度是 .
(4)若该实验中学共有学生3000人,请据此估计该校最喜欢“老家河南”主题线路的学生有多少人.