题目内容
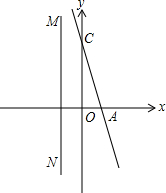 如图,一次函数y=kx+n的图象分别交x轴、y轴与A、C两点.且C点的坐标为(0,3),OC=3OA,直线MN经过点(-1,0)且与x轴垂直,
如图,一次函数y=kx+n的图象分别交x轴、y轴与A、C两点.且C点的坐标为(0,3),OC=3OA,直线MN经过点(-1,0)且与x轴垂直,(1)求一次函数的解析式;
(2)将y=kx+n向下平移m个单位,设平移后的直线与y轴交于点D,与直线MN交于点E.
①当m=
| 10 | 3 |
②四边形ADEC能否为菱形?若能,直接写出移动的单位长度.
分析:(1)先根据C点的坐标为(0,3),OC=3OA求出A点坐标,把AC两点的坐标代入一次函数y=kx+n即可得出k、n的值,故可得出一次函数的解析式;
(2)①根据平移的性质得出m=
时直线的解析式,求出DE两点的坐标,进而可得出结论;
②设直线移动m个单位长度四边形ADEC为菱形,再用m表示出E点坐标,根据菱形的性质即可得出结论.
(2)①根据平移的性质得出m=
| 10 |
| 3 |
②设直线移动m个单位长度四边形ADEC为菱形,再用m表示出E点坐标,根据菱形的性质即可得出结论.
解答: 解:(1)∵C点的坐标为(0,3),OC=3OA,
解:(1)∵C点的坐标为(0,3),OC=3OA,
∴A(1,0),
∵
,
解得
.
∴一次函数的解析式为:y=-3x+3;
(2)①∵一次函数的解析式为y=-3x+3,
∴向下平移
个单位时的解析式为y=-3x-
,
∴D(0,-
),E(-1,
),
∵直线DE由直线AC平移而来,
∵AC∥DE,
∵AC2=OA2+OC2=12+32=10,DE2=12+(-
-
)2=10,
∴AC=DE,
∴四边形ADEC是平行四边形;
②能.
设直线移动m个单位长度四边形ADEC为菱形,
∵一次函数的解析式为:y=-3x+3,
∴移动后直线的解析式为y=-3x+3-m,
∵平移后的直线与y轴交于点D,与直线MN交于点E,
∴D(0,3-m),E(-1,6-m),
∵∵直线DE由直线AC平移而来,
∵AC∥DE,
∵AC2=OA2+OC2=12+32=10,DE2=12+(3-m-6+m)2=10,
∴AC=DE,
∴四边形ADEC是平行四边形,
∵四边形ADEC为菱形,
∴CE=AC,即CE2=AC2=10,
∵C(0,3),E(-1,6-m),
∴CE2=12+(3-6+m)2=10,解得m=6或m=0,
∴当直线向下或向上移动6个单位时,四边形ADEC为菱形.
 解:(1)∵C点的坐标为(0,3),OC=3OA,
解:(1)∵C点的坐标为(0,3),OC=3OA,∴A(1,0),
∵
|
解得
|
∴一次函数的解析式为:y=-3x+3;
(2)①∵一次函数的解析式为y=-3x+3,
∴向下平移
| 10 |
| 3 |
| 1 |
| 3 |
∴D(0,-
| 1 |
| 3 |
| 8 |
| 3 |
∵直线DE由直线AC平移而来,
∵AC∥DE,
∵AC2=OA2+OC2=12+32=10,DE2=12+(-
| 1 |
| 3 |
| 8 |
| 3 |
∴AC=DE,
∴四边形ADEC是平行四边形;
②能.
设直线移动m个单位长度四边形ADEC为菱形,
∵一次函数的解析式为:y=-3x+3,
∴移动后直线的解析式为y=-3x+3-m,
∵平移后的直线与y轴交于点D,与直线MN交于点E,
∴D(0,3-m),E(-1,6-m),
∵∵直线DE由直线AC平移而来,
∵AC∥DE,
∵AC2=OA2+OC2=12+32=10,DE2=12+(3-m-6+m)2=10,
∴AC=DE,
∴四边形ADEC是平行四边形,
∵四边形ADEC为菱形,
∴CE=AC,即CE2=AC2=10,
∵C(0,3),E(-1,6-m),
∴CE2=12+(3-6+m)2=10,解得m=6或m=0,
∴当直线向下或向上移动6个单位时,四边形ADEC为菱形.
点评:本题考查的是一次函数综合题,涉及到平行四边形及菱形的判定与性质,综合性较强,难度适中.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知,如图,一次函数y1=-x-1与反比例函数y2=-
已知,如图,一次函数y1=-x-1与反比例函数y2=-| 2 |
| x |
| A、x>1 |
| B、x<-2或0<x<1 |
| C、-2<x<1 |
| D、-2<x<0或x>1 |
 如图,一次函数y=kx+2的图象与反比例函数y=
如图,一次函数y=kx+2的图象与反比例函数y= 13、如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是
13、如图,一次函数y=kx+b(k<0)的图象经过点A.当y<3时,x的取值范围是 (2013•成都)如图,一次函数y1=x+1的图象与反比例函数
(2013•成都)如图,一次函数y1=x+1的图象与反比例函数 如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数
如图,一次函数y=x+3的图象与x轴、y轴分别交于点A、点B,与反比例函数