题目内容
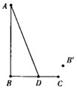
如图,在梯形ABCD中,AB∥DC,∠ABC=90°,AB=2,BC=4,tan∠ADC=2.

(1)求证:DC=BC;
(2)E是梯形内一点,连接DE、CE,将△DCE绕点C顺时针旋转90°,得△BCF,连接EF.判断EF与CE的数量关系,并证明你的结论;
(3)在(2)的条件下,当CE=2BE,∠BEC=135°时,求cos∠BFE的值.

(1)求证:DC=BC;
(2)E是梯形内一点,连接DE、CE,将△DCE绕点C顺时针旋转90°,得△BCF,连接EF.判断EF与CE的数量关系,并证明你的结论;
(3)在(2)的条件下,当CE=2BE,∠BEC=135°时,求cos∠BFE的值.
(1)证明见解析(2)EF=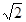 CE.证明见解析(3)
CE.证明见解析(3)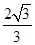
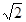 CE.证明见解析(3)
CE.证明见解析(3)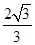
(1)证明:作AP⊥DC于点P.
∵AB∥CD,∠ABC=90°,
∴四边形APCB是矩形,………………………………1分
∴PC=AB=2,AP=BC=4.
在Rt△ADP中,tan∠ADC=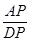 即
即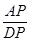 =2,
=2,
∴DP=2,
∴DC=DP+PC=4=BC.…………………………3分
(2)EF=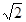 CE.………………………4分
CE.………………………4分
证明如下:
由△DCE绕点C顺时针旋转90°得△BCF,
∴CF=CE,∠ECF=90°,
∴EF= . …………………………6分
. …………………………6分
(3)由(2)得∠CEF=45°.
∵∠BEC=135°,
∴∠BEF=90°. ………………………………7分
设BE=a,则CE=2a,由EF=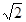 CE,则EF=
CE,则EF=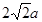
在Rt△BEF中,由勾股定理得:BF=3a,
∴COS∠BFE=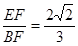 . ……………………10分
. ……………………10分
(1)如图,过A作AP⊥DC于点P,由AB∥CD可以得到∠ABC=90°,然后得到四边形APCB是矩形,接着利用已知条件可以求出PC=AB=2,AP=BC=4,又在Rt△ADP中,根据tan∠ADC=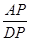 可以求出DP=2,接着得到DC=4,由此即可解决问题;
可以求出DP=2,接着得到DC=4,由此即可解决问题;
(2)EF=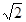 CE.由△DCE绕点C顺时针旋转90°得△BCF,根据旋转的性质得到CF=CE,∠ECF=90°,然后利用勾股定理即可求出EF;
CE.由△DCE绕点C顺时针旋转90°得△BCF,根据旋转的性质得到CF=CE,∠ECF=90°,然后利用勾股定理即可求出EF;
(3)由(2)得∠CEF=45°,而∠BEC=135°,由此得到∠BEF=90°.设BE=a,则CE=2a,由EF=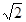 CE,则EF=2
CE,则EF=2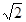 a.在Rt△BEF中,由勾股定理得:BF=3a,然后根据余弦的定义即可求解.
a.在Rt△BEF中,由勾股定理得:BF=3a,然后根据余弦的定义即可求解.
∵AB∥CD,∠ABC=90°,
∴四边形APCB是矩形,………………………………1分
∴PC=AB=2,AP=BC=4.
在Rt△ADP中,tan∠ADC=
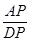 即
即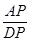 =2,
=2,∴DP=2,
∴DC=DP+PC=4=BC.…………………………3分
(2)EF=
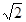 CE.………………………4分
CE.………………………4分证明如下:
由△DCE绕点C顺时针旋转90°得△BCF,
∴CF=CE,∠ECF=90°,
∴EF=
 . …………………………6分
. …………………………6分(3)由(2)得∠CEF=45°.
∵∠BEC=135°,
∴∠BEF=90°. ………………………………7分
设BE=a,则CE=2a,由EF=
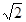 CE,则EF=
CE,则EF=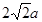
在Rt△BEF中,由勾股定理得:BF=3a,
∴COS∠BFE=
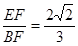 . ……………………10分
. ……………………10分(1)如图,过A作AP⊥DC于点P,由AB∥CD可以得到∠ABC=90°,然后得到四边形APCB是矩形,接着利用已知条件可以求出PC=AB=2,AP=BC=4,又在Rt△ADP中,根据tan∠ADC=
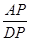 可以求出DP=2,接着得到DC=4,由此即可解决问题;
可以求出DP=2,接着得到DC=4,由此即可解决问题;(2)EF=
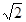 CE.由△DCE绕点C顺时针旋转90°得△BCF,根据旋转的性质得到CF=CE,∠ECF=90°,然后利用勾股定理即可求出EF;
CE.由△DCE绕点C顺时针旋转90°得△BCF,根据旋转的性质得到CF=CE,∠ECF=90°,然后利用勾股定理即可求出EF;(3)由(2)得∠CEF=45°,而∠BEC=135°,由此得到∠BEF=90°.设BE=a,则CE=2a,由EF=
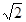 CE,则EF=2
CE,则EF=2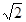 a.在Rt△BEF中,由勾股定理得:BF=3a,然后根据余弦的定义即可求解.
a.在Rt△BEF中,由勾股定理得:BF=3a,然后根据余弦的定义即可求解.
练习册系列答案
相关题目

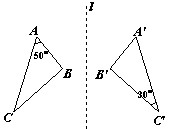



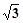 cm,点D是线段BC上的一个动点,连接AD,动点B′始终保持与点B关于直线AD对称,当点D由点B位置向右运动至点C位置时,相应的点B′所经过的路程为 cm。
cm,点D是线段BC上的一个动点,连接AD,动点B′始终保持与点B关于直线AD对称,当点D由点B位置向右运动至点C位置时,相应的点B′所经过的路程为 cm。