题目内容
18．下列计算：①$\sqrt{25}$=5；②$\root{3}{-\frac{1}{27}}$=$±\frac{1}{3}$；③$\sqrt{（-2）^{2}}$=-2；④（-$\sqrt{3}$）2=3；⑤$\sqrt{1\frac{25}{144}}$=1$\frac{5}{12}$，其中正确的个数有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
分析 依据算术平方根、立方根、二次根式的性质进行判断即可．
解答 解：①$\sqrt{25}$=5，故①正确；
②$\root{3}{-\frac{1}{27}}$=-$\frac{1}{3}$，故②错误；
③$\sqrt{（-2）^{2}}$=2，故③错误；
④（-$\sqrt{3}$）2=3，故④正确；
⑤$\sqrt{1\frac{25}{144}}$=$\sqrt{\frac{169}{144}}$=$\frac{13}{12}$，⑤错误．
故选：B．
点评 本题主要考查的是实数的运算，熟练掌握实数的运算性质是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
1．下列各运算中，计算正确的是（ ）
| A． | （x-2）2=x2-4 | B． | （3a2）3=9a6 | C． | x6÷x2=x3 | D． | x3•x2=x5 |
如图是由4个大小相同的正方体组合而成的几何体，其俯视图是（ ）
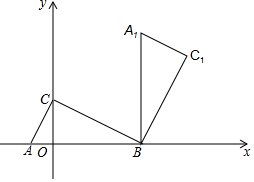如图，在平面直角坐标系中，△ABC三个顶点坐标分别为A（-1，0）、B（4，0）、C（0，2），将△ABC绕点B顺时针旋转90°得到△A1BC1，有一条抛物线经过点A，且它的顶点为A1．
3．若分式$\frac{{{x^2}-1}}{{{x^2}-2x-3}}$的值为0，则x的值为（ ）
| A． | -1 | B． | 1 | C． | ±1 | D． | 0 |