题目内容
在直角三角形中,自两锐角所引的两条中线长分别为5和2
,则斜边长为( )
| 10 |
| A、10 | ||
B、4
| ||
C、
| ||
D、2
|
分析:根据已知设AC=x,BC=y,在Rt△ACD和Rt△BCE中,根据勾股定理分别列等式,从而求得AC,BC的长,最后根据勾股定理即可求得AB的长.
解答: 解:如图,在△ABC中,∠C=90°,AD、BE为△ABC的两条中线,且AD=2
解:如图,在△ABC中,∠C=90°,AD、BE为△ABC的两条中线,且AD=2
,BE=5,求AB的长.
设AC=x,BC=y
根据勾股定理得:
在Rt△ACD中,x2+(
y)2=(2
)2
在Rt△BCE中,(
x)2+y2=52
解之得,x=6,y=4
∴在Rt△ABC中,AB=
=2
,
故选D.
 解:如图,在△ABC中,∠C=90°,AD、BE为△ABC的两条中线,且AD=2
解:如图,在△ABC中,∠C=90°,AD、BE为△ABC的两条中线,且AD=2| 10 |
设AC=x,BC=y
根据勾股定理得:
在Rt△ACD中,x2+(
| 1 |
| 2 |
| 10 |
在Rt△BCE中,(
| 1 |
| 2 |
解之得,x=6,y=4
∴在Rt△ABC中,AB=
| 62+42 |
| 13 |
故选D.
点评:本题主要涉及的知识点:中线的定义、勾股定理.

练习册系列答案
相关题目
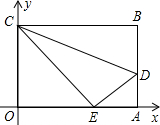 上的点E处.
上的点E处. ,则斜边长为
,则斜边长为