题目内容
等腰三角形ABC中,AB=AC,AD是角平分线,则“①AD⊥BC,②BD=DC,③∠B=∠C,④∠BAD=∠CAD”中,结论正确的个数是
- A.4
- B.3
- C.2
- D.1
A
试题分析:根据等边对等角,“三线合一”:等腰三角形的顶角平分线、底边上的高和底边上的中线重合,依次分析各小题即可。
∵AB=AC,AD是角平分线,
根据“三线合一”可得AD⊥BC,BD=DC,
∵AB=AC,
∴∠B=∠C,
∵AD是角平分线,
∴∠BAD=∠CAD
结论正确是①②③④共4个,故选A.
考点:本题考查了等腰三角形的性质
点评:解答本题的关键是掌握好等腰三角形的性质:①等边对等角;②“三线合一”.
试题分析:根据等边对等角,“三线合一”:等腰三角形的顶角平分线、底边上的高和底边上的中线重合,依次分析各小题即可。
∵AB=AC,AD是角平分线,
根据“三线合一”可得AD⊥BC,BD=DC,
∵AB=AC,
∴∠B=∠C,
∵AD是角平分线,
∴∠BAD=∠CAD
结论正确是①②③④共4个,故选A.
考点:本题考查了等腰三角形的性质
点评:解答本题的关键是掌握好等腰三角形的性质:①等边对等角;②“三线合一”.

练习册系列答案
相关题目
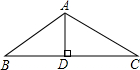 如图所示,在等腰三角形ABC中,AB=AC=12cm,∠ABC=30°,那么底边上的高AD=
如图所示,在等腰三角形ABC中,AB=AC=12cm,∠ABC=30°,那么底边上的高AD= 如图,等腰三角形ABC中,AB=AC,AD是底边BC上的中线,若AB=10,BC=12,则中线AD的长度为( )
如图,等腰三角形ABC中,AB=AC,AD是底边BC上的中线,若AB=10,BC=12,则中线AD的长度为( )