题目内容
已知a,b均为不超过4的正整数,b≠2a,关于x,y的方程组
|
分析:根据a,b均为不超过4的正整数且为b≠2a,得到a、b的所有组合,代入方程组,解出所有方程组的解,舍去解为负值的情况即可得到a、b的值.
解答:解:因为a,b均为不超过4的正整数且为b≠2a,所以可有以下组合:
a=1,b=3;a=1,b=1;a=1,b=4;
a=2,b=1;a=2,b=2;a=2,b=3;
a=3,b=1;a=3,b=2;a=3,b=3;a=3,b=4;
a=4,b=1;a=4,b=2;a=4,b=3;a=4,b=4.组成方程组解答即可.
(1)
,解得
(0,舍去);(2)
,解得
(负值舍去);
(3)
,解得
;(4)
,解得
;
(5)
,解得
;(6)
,解得
;
(7)
,解得
;(8)
,解得
;
(9)
,解得
;(舍去)(10)
,解得
(负值舍去);
(11)
,解得
;(12)
,解得
;
(13)
,解得
;(舍去)(14)
,解得
(负值舍去)
故a、b的所有整数值a=1,b=3;a=1,b=4;a=2,b=1;a=2,b=2;a=2,b=3;a=3,b=1;a=3,b=2;a=3,b=3;a=4,b=1;a=4,b=2;a=4,b=3.
a=1,b=3;a=1,b=1;a=1,b=4;
a=2,b=1;a=2,b=2;a=2,b=3;
a=3,b=1;a=3,b=2;a=3,b=3;a=3,b=4;
a=4,b=1;a=4,b=2;a=4,b=3;a=4,b=4.组成方程组解答即可.
(1)
|
|
|
|
(3)
|
|
|
|
(5)
|
|
|
|
(7)
|
|
|
|
(9)
|
|
|
|
(11)
|
|
|
|
(13)
|
|
|
|
故a、b的所有整数值a=1,b=3;a=1,b=4;a=2,b=1;a=2,b=2;a=2,b=3;a=3,b=1;a=3,b=2;a=3,b=3;a=4,b=1;a=4,b=2;a=4,b=3.
点评:此题考查了解二元一次方程组,根据题目条件列出a、b的所有情况是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
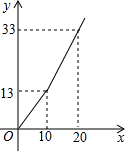 为了鼓励市民节约用水,市政府制定了新的收费标准:设用水量为x吨,需付水费为y元,y与x的函数图象如图.
为了鼓励市民节约用水,市政府制定了新的收费标准:设用水量为x吨,需付水费为y元,y与x的函数图象如图.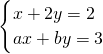 只有正数解,求a,b的所有可能值.
只有正数解,求a,b的所有可能值.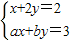 只有正数解,求a,b的所有可能值.
只有正数解,求a,b的所有可能值.