题目内容
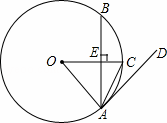
如图，在⊙O中，半径OC垂直于弦AB，垂足为点E．若点D在⊙O的外且∠DAC=∠BAC，求证：直线AD是⊙O的切线．
证明：∵半径OC垂直于弦AB，
∴∠OCA+∠CAE=90°，
∵CO=OA，
∴∠OCA=∠OAC，
∵∠DAC=∠BAC，
∴∠DAC+∠OAC=90°，
∴OA⊥AD，
即直线AD是⊙O的切线．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
口算题卡北京妇女儿童出版社系列答案题目内容
如图，在⊙O中，半径OC垂直于弦AB，垂足为点E．若点D在⊙O的外且∠DAC=∠BAC，求证：直线AD是⊙O的切线．
证明：∵半径OC垂直于弦AB，
∴∠OCA+∠CAE=90°，
∵CO=OA，
∴∠OCA=∠OAC，
∵∠DAC=∠BAC，
∴∠DAC+∠OAC=90°，
∴OA⊥AD，
即直线AD是⊙O的切线．
口算题卡北京妇女儿童出版社系列答案
﹣
的结果是 ．
B．－
D． m>
的图像经过点
，
，且与正比例函数
的图像相交于点
，
．
的
值；
的解析式；
轴所围成的三角形面积．(画
图解答)