题目内容
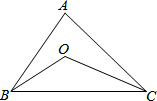如图，已知∠ABO=20°，∠ACO=25°，∠A=55°，则∠BOC等于（ ）分析：延长BO交AC于点D，由三角形外角的性质可得出∠ODC的度数，进而可得出结论．
解答：
解：延长BO交AC于点D，
∵∠ABO=20°，∠A=55°，∠ODC是△ABD的外角，
∴∠ODC=∠A+∠ABO=55°+20°=75°，
同理，∵∠BOC是△ODC的外角，∠ACO=25°，
∴∠BOC=∠ODC+∠ACO=75°+25°=100°．
故选B．
解：延长BO交AC于点D，∵∠ABO=20°，∠A=55°，∠ODC是△ABD的外角，
∴∠ODC=∠A+∠ABO=55°+20°=75°，
同理，∵∠BOC是△ODC的外角，∠ACO=25°，
∴∠BOC=∠ODC+∠ACO=75°+25°=100°．
故选B．
点评：本题考查的是三角形外角的性质，熟知三角形的外角等于与之不相邻的两个内角的和是解答此题的关键．
练习册系列答案
小学夺冠AB卷系列答案
相关题目
13、如图，已知∠ABO=30°，以O为圆心2cm为半径作圆O，当OB=
如图，已知△ABO的顶点A和AB边的中点C都在双曲线y=
如图，已知△ABO的三个顶点的坐标分别为A（-1，3），B（-5，0），O（0，0）．
如图，已知△ABO的顶点A和AB边的中点C都在双曲线y=
如图，已知△ABO，画出它关于x轴和y轴的对称图形．