题目内容
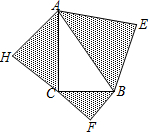 已知:如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中阴影部分的面积为
已知:如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=3,则图中阴影部分的面积为分析:先用直角三角形的边长表示出阴影部分的面积,再根据勾股定理可得:AB2=AC2+BC2,进而可将阴影部分的面积求出.
解答:解:在Rt△ABC中,AB2=AC2+BC2,AB=3,
S阴影=S△AHC+S△BFC+S△AEB
=
×(
)2+
×(
)2+
×(
)2
=
(AC2+BC2+AB2)
=
AB2,
=
×32
=
.
故图中阴影部分的面积为
.
S阴影=S△AHC+S△BFC+S△AEB
=
| 1 |
| 2 |
| AC | ||
|
| 1 |
| 2 |
| BC | ||
|
| 1 |
| 2 |
| AB | ||
|
=
| 1 |
| 4 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 9 |
| 2 |
故图中阴影部分的面积为
| 9 |
| 2 |
点评:本题主要是考查勾股定理的应用,比较简单.
注意:以直角三角形的两条直角边为斜边的两个等腰直角三角形的面积的和等于以斜边为斜边的等腰直角三角形的面积;等腰直角三角形的斜边是直角边的
倍.
注意:以直角三角形的两条直角边为斜边的两个等腰直角三角形的面积的和等于以斜边为斜边的等腰直角三角形的面积;等腰直角三角形的斜边是直角边的
| 2 |

练习册系列答案
相关题目
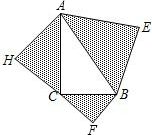 已知:如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=6,则图中阴影部分的面积为
已知:如图,以Rt△ABC的三边为斜边分别向外作等腰直角三角形.若斜边AB=6,则图中阴影部分的面积为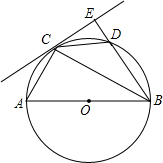 已知:如图,以Rt△ABC的斜边AB为直径作⊙O,D是⊙O上的点,且有AC=CD.过点C作⊙O的切线,与BD的延长线交于点E,连接CD.
已知:如图,以Rt△ABC的斜边AB为直径作⊙O,D是⊙O上的点,且有AC=CD.过点C作⊙O的切线,与BD的延长线交于点E,连接CD. 已知,如图,以Rt△ABC的斜边AB为直径作⊙0,D是BC上的点,且有弧AC=弧CD,连CD、BD,在BD延长线上取一点E,使∠DCE=∠CBD.
已知,如图,以Rt△ABC的斜边AB为直径作⊙0,D是BC上的点,且有弧AC=弧CD,连CD、BD,在BD延长线上取一点E,使∠DCE=∠CBD. 已知:如图,以Rt△ABC的直角边AC为直径作⊙O,交AB于D点,OE∥AB交BC于E点,求证:DE为⊙O的切线.
已知:如图,以Rt△ABC的直角边AC为直径作⊙O,交AB于D点,OE∥AB交BC于E点,求证:DE为⊙O的切线.