题目内容
y=-x与 交于A,C两点,分别过A,C作x轴的垂线,垂足分别为A.B,
交于A,C两点,分别过A,C作x轴的垂线,垂足分别为A.B,(1)求A,C的点的坐标;
(2)求四边形ABCD的面积.

【答案】分析:(1)求出两函数组成的方程组的解,即可得出A、C的坐标;
(2)根据A、C的坐标求出AB、CD、BD的值,分别求出△ABD和△CDB的面积,即可求出答案.
解答:(1)解:解方程组 得:
得:
-x=- ,
,
解得x=±1,
当x=1时,y=-1,
当x=-1时,y=1,
∵A在第二象限,C在第四象限,
∴A(-1,1),C(1,-1);
(2)解:∵A(-1,1),C(1,-1),AB⊥x轴,CD⊥x轴,
∴AB=1,OB=|-1|=1,OD=1,CD|-1|=1,
∴BD=1+1=2,
∴S四边形ABCD=S△ABD+S△CDB
= ×2×1+
×2×1+ ×2×1
×2×1
=2.
点评:本题考查了解方程组,一次函数与反比例函数的交点问题,三角形的面积等知识点,解此题的关键是求出A、C的坐标,题目比较典型,是一道比较好的题目.
(2)根据A、C的坐标求出AB、CD、BD的值,分别求出△ABD和△CDB的面积,即可求出答案.
解答:(1)解:解方程组
 得:
得:-x=-
 ,
,解得x=±1,
当x=1时,y=-1,
当x=-1时,y=1,
∵A在第二象限,C在第四象限,
∴A(-1,1),C(1,-1);
(2)解:∵A(-1,1),C(1,-1),AB⊥x轴,CD⊥x轴,
∴AB=1,OB=|-1|=1,OD=1,CD|-1|=1,
∴BD=1+1=2,
∴S四边形ABCD=S△ABD+S△CDB
=
 ×2×1+
×2×1+ ×2×1
×2×1=2.
点评:本题考查了解方程组,一次函数与反比例函数的交点问题,三角形的面积等知识点,解此题的关键是求出A、C的坐标,题目比较典型,是一道比较好的题目.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目


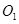 与⊙
与⊙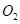 相交于
相交于 、
、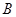 两点,点
两点,点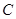 为⊙
为⊙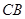 与⊙
与⊙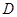 。
。
 是⊙
是⊙ ;(4分)
;(4分)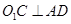 ;(4分)
;(4分) 为
为 的直径,
的直径, ,垂足为
,垂足为 ,
, ,
, 与
与 交于
交于 .
.
 ;
; ,
, 把半圆三等分,
把半圆三等分, ,求
,求 的长.
的长. (
( )与x轴、y轴分别交于A、B两点,∠ABO=60°.经过A、O两点的⊙O1与x轴的负半轴交于点C,与直线AB切于点A.
)与x轴、y轴分别交于A、B两点,∠ABO=60°.经过A、O两点的⊙O1与x轴的负半轴交于点C,与直线AB切于点A. 作直线EF∥y轴,在直线EF上是否存在一点D,使得△DAB的周长最短,若存在,求出D点坐标,不存在,说明理由;
作直线EF∥y轴,在直线EF上是否存在一点D,使得△DAB的周长最短,若存在,求出D点坐标,不存在,说明理由; 与⊙
与⊙ 的值是否发生变化,若不变,求其值,若发生变化,求出其值的变化范围.
的值是否发生变化,若不变,求其值,若发生变化,求出其值的变化范围.

