题目内容
在直角坐标系中,A点的坐标为(1,
),将线段OA绕坐标原点O逆时针旋转90°,得 到线段OB.
到线段OB.
(1)求B点的坐标;
(2)除了可以由线段OA旋转变换得到OB以外,还能不能由线段OA作轴对称变换得到OB?若能由轴对称变换得到,请求出该对称轴的解析式;若不能,请说明理由.
| 3 |
 到线段OB.
到线段OB.(1)求B点的坐标;
(2)除了可以由线段OA旋转变换得到OB以外,还能不能由线段OA作轴对称变换得到OB?若能由轴对称变换得到,请求出该对称轴的解析式;若不能,请说明理由.
分析:(1)因为A点的坐标为(1,
),将线段OA绕坐标原点O逆时针旋转90°,得到线段OB,要求B点的坐标,所以可作AM⊥ox轴于M,作BN⊥ox轴于N,因为∠AOB=90°,所以∠OAM=∠BON,且OA=OB,所以Rt△AMO≌Rt△ONB,结合A点的坐标可求出BN=1,ON=
,又因点B在第二象限,所以点B的坐标为(-
,1);
(2)能够由轴对称变换得到:因为OA=OB,所以对称轴为过O的AB的中垂线,利用A、B的坐标,可求出AB的中点C的坐标,进而设对称轴的解析式为y=kx,将点C的坐标代入即可求得k=-2-
,进而求出解析式.
| 3 |
| 3 |
| 3 |
(2)能够由轴对称变换得到:因为OA=OB,所以对称轴为过O的AB的中垂线,利用A、B的坐标,可求出AB的中点C的坐标,进而设对称轴的解析式为y=kx,将点C的坐标代入即可求得k=-2-
| 3 |
解答: 解:(1)作AM⊥ox轴于M,作BN⊥ox轴于N,
解:(1)作AM⊥ox轴于M,作BN⊥ox轴于N,
因为∠AOB=90°,所以∠OAM=∠BON,
且OA=OB,所以Rt△AMO≌Rt△ONB(3分)
因为A点的坐标为(1,
),所以BN=1,ON=
,
而点B在第二象限,所以点B的坐标为(-
,1),(5分)
(2)能够由轴对称变换得到:因为OA=OB,所以对称轴为AB的中垂线,(6分)
可以求出AB的中点C的坐标为(
,
),(8分)
设对称轴的解析式为y=kx,将点C(
,
)代入得k=-2-
,
则对称轴OC的解析为y=(-2-
)x.(10分)
 解:(1)作AM⊥ox轴于M,作BN⊥ox轴于N,
解:(1)作AM⊥ox轴于M,作BN⊥ox轴于N,因为∠AOB=90°,所以∠OAM=∠BON,
且OA=OB,所以Rt△AMO≌Rt△ONB(3分)
因为A点的坐标为(1,
| 3 |
| 3 |
而点B在第二象限,所以点B的坐标为(-
| 3 |
(2)能够由轴对称变换得到:因为OA=OB,所以对称轴为AB的中垂线,(6分)
可以求出AB的中点C的坐标为(
1-
| ||
| 2 |
1+
| ||
| 2 |
设对称轴的解析式为y=kx,将点C(
1-
| ||
| 2 |
1+
| ||
| 2 |
| 3 |
则对称轴OC的解析为y=(-2-
| 3 |
点评:本题的解决需用到数形结合、方程和转化等数学思想方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
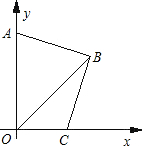 如图,在直角坐标系中,B点的坐标为(a,b),且a、b满足
如图,在直角坐标系中,B点的坐标为(a,b),且a、b满足