Question

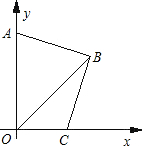如图，在直角坐标系中，B点的坐标为（a，b），且a、b满足

a+b-4

+(a-b)2=0．
（1）求B点的坐标；
（2）点A为y轴上一动点，过B点作BC⊥AB交x轴正半轴于点C，求证：BA=BC．

Answer 1

分析：（1）由于所给的等式是两个非负数的和是0，根据非负数的性质得到每一个非负数都等于0，从而得到一个关于a，b的二元一次方程组，解之即可．
（2）作BM⊥y轴于M，BN⊥x轴于N点，很容易知道△ABM≌△CBN．而B点坐标是（2，2），那么就有一组对应边相等，故全等，可得BA=BC．

解答：解：（1）∵

a+b-4

≥0，（a-b）²≥0，
而

a+b-4

+(a-b)2=0
∴

a+b-4

=0，（a-b）²=0
∴

a+b-4=0 a-b=0

．解得

a=2 b=2

．
∴B点坐标为（2，2）；

（2）作BM⊥y轴于M，BN⊥x轴于N点，如图：
∴∠MBN=90°．
∵BC⊥AB，
∴∠ABC=90°．
∴∠ABM=∠CBN．
∵B点坐标是（2，2），
∴BM=BN，
在△ABM和△CBN中，

∠AMB=∠BNC ∠ABM=∠CBN BM=BN

，
∴△ABM≌△CBN．
∴BA=BC．

点评：本题主要考查了非负数的性质，主要利用了两个非负数的和是0，则每一个非负数都等于0，也利用了全等三角形的判定（ASA）和性质．