题目内容
2.已知x2-2015x+1=0,(1)求x-$\frac{1}{x}$(x>1)的值;
(2)$\frac{{x}^{2}}{{x}^{4}+{x}^{2}+1}$+$\frac{2015x}{{x}^{2}+1}$的值.
分析 (1)先把等式两边除以x得到x+$\frac{1}{x}$=2015,再利用完全平方公式变形得x-$\frac{1}{x}$=$\sqrt{(x+\frac{1}{x})^{2}-4}$,然后利用整体代入的方法计算;
(2)利用分式的性质和整体代入的方法得到原式=$\frac{1}{{x}^{2}+1+\frac{1}{{x}^{2}}}$+$\frac{2015x}{2015x}$,再利用完全平方公式变形得到$\frac{1}{(x+\frac{1}{x})^{2}-1}$+1,然后再利用整体代入的方法计算.
解答 解:(1)∵x2-2015x+1=0,
∴x-2015+$\frac{1}{x}$=0,
∴x+$\frac{1}{x}$=2015,
∴x-$\frac{1}{x}$=$\sqrt{(x-\frac{1}{x})^{2}}$(x>1)
=$\sqrt{(x+\frac{1}{x})^{2}-4}$
=$\sqrt{201{5}^{2}-4}$
=$\sqrt{4060221}$;
(2)原式=$\frac{1}{{x}^{2}+1+\frac{1}{{x}^{2}}}$+$\frac{2015x}{2015x}$
=$\frac{1}{(x+\frac{1}{x})^{2}-1}$+1
=$\frac{1}{201{5}^{2}-1}$+1
=1$\frac{1}{4060224}$.
点评 本题考查了分式的化简求值:把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.抛物线的对称轴为直线x=3,y的最大值为-5,且与y=$\frac{1}{2}$x2的图象开口大小相同.则这条抛物线解析式为( )
| A. | y=-$\frac{1}{2}$(x+3)2+5 | B. | y=-$\frac{1}{2}$(x-3)2-5 | C. | y=$\frac{1}{2}$(x+3)2+5 | D. | y=$\frac{1}{2}$(x-3)2-5 |
 如图,已知∠α,
如图,已知∠α,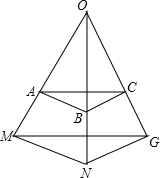 如图,已知AB∥MN,BC∥NG.求证:$\frac{OA}{OM}$=$\frac{OC}{OG}$.
如图,已知AB∥MN,BC∥NG.求证:$\frac{OA}{OM}$=$\frac{OC}{OG}$.