题目内容
 如图,B为双曲线
如图,B为双曲线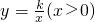 上一点,直线AB平行于y轴交直线y=x于点A,若OB2-AB2=4,则k=________.
上一点,直线AB平行于y轴交直线y=x于点A,若OB2-AB2=4,则k=________.
2
分析:延长AB交x轴于点C,则AC⊥OC,AC=OC.设A(a,a),则C(a,0),B(a, ).运用勾股定理及平方差公式将OB2-AB2变形为BC(BC+AC+AB),再用含a,k的代数式表示,根据OB2-AB2=4,从而求出k的值.
).运用勾股定理及平方差公式将OB2-AB2变形为BC(BC+AC+AB),再用含a,k的代数式表示,根据OB2-AB2=4,从而求出k的值.
解答: 解:延长AB交x轴于点C,则AC⊥OC,AC=OC.
解:延长AB交x轴于点C,则AC⊥OC,AC=OC.
设A(a,a),则C(a,0),B(a, ).
).
∵OB2-AB2=4,OB2=BC2+OC2,
∴BC2+OC2-AB2=4,
∵AC=OC,
∴BC2+AC2-AB2=4,
∴BC2+(AC+AB)(AC-AB)=4,
∴BC2+BC(AC+AB)=4,
∴BC(BC+AC+AB)=4,
∴ (
( +a+a-
+a+a- )=4,
)=4,
∴2k=4,
k=2.
故答案为:2.
点评:本题考查反比例函数、正比例函数的图象性质,代数式的恒等变形等知识,利用形数结合解决此类问题,是非常有效的方法.
分析:延长AB交x轴于点C,则AC⊥OC,AC=OC.设A(a,a),则C(a,0),B(a,
 ).运用勾股定理及平方差公式将OB2-AB2变形为BC(BC+AC+AB),再用含a,k的代数式表示,根据OB2-AB2=4,从而求出k的值.
).运用勾股定理及平方差公式将OB2-AB2变形为BC(BC+AC+AB),再用含a,k的代数式表示,根据OB2-AB2=4,从而求出k的值.解答:
 解:延长AB交x轴于点C,则AC⊥OC,AC=OC.
解:延长AB交x轴于点C,则AC⊥OC,AC=OC.设A(a,a),则C(a,0),B(a,
 ).
).∵OB2-AB2=4,OB2=BC2+OC2,
∴BC2+OC2-AB2=4,
∵AC=OC,
∴BC2+AC2-AB2=4,
∴BC2+(AC+AB)(AC-AB)=4,
∴BC2+BC(AC+AB)=4,
∴BC(BC+AC+AB)=4,
∴
 (
( +a+a-
+a+a- )=4,
)=4,∴2k=4,
k=2.
故答案为:2.
点评:本题考查反比例函数、正比例函数的图象性质,代数式的恒等变形等知识,利用形数结合解决此类问题,是非常有效的方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
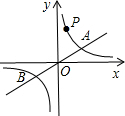

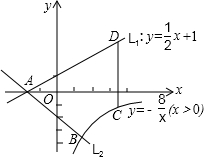 时,点A、B、C、D围成的四边形面积.
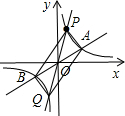
时,点A、B、C、D围成的四边形面积. (2013•海沧区一模)如图,已知双曲线
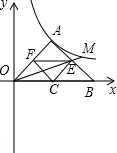
(2013•海沧区一模)如图,已知双曲线 (2005•东城区一模)如图,A为双曲线
(2005•东城区一模)如图,A为双曲线