题目内容
如图,在边长为2的正方形ABCD中,以点D为圆心、DC为半径作 ,点E在AB上,且与A、B两点均不重合,点M在AD上,且ME=MD,过点E作EF⊥ME,交BC于点F,连接DE、MF.
,点E在AB上,且与A、B两点均不重合,点M在AD上,且ME=MD,过点E作EF⊥ME,交BC于点F,连接DE、MF.(1)求证:EF是
 所在⊙D的切线;
所在⊙D的切线;(2)当MA=
 时,求MF的长;
时,求MF的长;(3)试探究:△MFE能否是等腰直角三角形?若是,请直接写出MF的长度;若不是,请说明理由.

【答案】分析:(1)过点D作DG⊥EF于G,根据等边对等角可得∠MDE=∠MED,然后根据等角的余角相等求出∠AED=∠GED,再利用“角角边”证明△ADE和△GDE全等,根据全等三角形对应边相等可得AD=GD,再根据切线的定义即可得证;
(2)求出ME=MD= ,然后利用勾股定理列式求出AE,再求出BE,根据同角的余角相等求出∠1=∠3,然后求出△AME和△BEF相似,根据相似三角形对应边成比例列式求出EF,再利用勾股定理列式计算即可得解;
,然后利用勾股定理列式求出AE,再求出BE,根据同角的余角相等求出∠1=∠3,然后求出△AME和△BEF相似,根据相似三角形对应边成比例列式求出EF,再利用勾股定理列式计算即可得解;
(3)假设△MFE能是等腰直角三角形,根据等腰直角三角形的性质可得ME=EF,先利用“角角边”证明△AME和△BEF全等,根据全等三角形对边角相等可得AM=BE,设AM=BE=x,然后表示出MD,AE,再根据ME=MD,从而得到ME=AE,根据直角三角形斜边大于直角边可知△MEF不可能是等腰直角三角形.
解答:(1)证明:过点D作DG⊥EF于G,
∵ME=MD,
∴∠MDE=∠MED,
∵EF⊥ME,
∴∠DME+∠GED=90°,
∵∠DAB=90°,
∴∠MDE+∠AED=90°,
∴∠AED=∠GED,
∵在△ADE和△GDE中,
 ,
,
∴△ADE≌△GDE(AAS),
∴AD=GD,
∵ 的半径为DC,即AD的长度,
的半径为DC,即AD的长度,
∴EF是 所在⊙D的切线;
所在⊙D的切线;
(2)MA= 时,ME=MD=2-
时,ME=MD=2- =
= ,
,
在Rt△AME中,AE= =
= =1,
=1,
∴BE=AB-AE=2-1=1,
∵EF⊥ME,
∴∠1+∠2=180°-90°=90°,
∵∠B=90°,
∴∠2+∠3=90°,
∴∠1=∠3,
又∵∠DAB=∠B=90°,
∴△AME∽△BEF,
∴ =
= ,
,
即 =
= ,
,
解得EF= ,
,
在Rt△MEF中,MF= =
= =
= ;
;
(3)假设△MFE能是等腰直角三角形,
则ME=EF,
∵在△AME和△BEF中,
 ,
,
∴△AME≌△BEF(AAS),
∴MA=BE,
设AM=BE=x,
则MD=AD-MA=2-x,AE=AB-BE=2-x,
∵ME=MD,
∴ME=2-x,
∴ME=AE,
∵ME、AE分别是Rt△AME的斜边与直角边,
∴ME≠AE,
∴假设不成立,
故△MFE不能是等腰直角三角形.
点评:本题考查了圆的综合题型,主要考查了圆的切线的判定,全等三角形的判定与性质,相似三角形的判定与性质,勾股定理的应用,综合性较强,难度较大,(3)证明得到直角三角形的斜边与直角边相等的矛盾是解题的关键.
(2)求出ME=MD=
 ,然后利用勾股定理列式求出AE,再求出BE,根据同角的余角相等求出∠1=∠3,然后求出△AME和△BEF相似,根据相似三角形对应边成比例列式求出EF,再利用勾股定理列式计算即可得解;
,然后利用勾股定理列式求出AE,再求出BE,根据同角的余角相等求出∠1=∠3,然后求出△AME和△BEF相似,根据相似三角形对应边成比例列式求出EF,再利用勾股定理列式计算即可得解;(3)假设△MFE能是等腰直角三角形,根据等腰直角三角形的性质可得ME=EF,先利用“角角边”证明△AME和△BEF全等,根据全等三角形对边角相等可得AM=BE,设AM=BE=x,然后表示出MD,AE,再根据ME=MD,从而得到ME=AE,根据直角三角形斜边大于直角边可知△MEF不可能是等腰直角三角形.
解答:(1)证明:过点D作DG⊥EF于G,
∵ME=MD,
∴∠MDE=∠MED,
∵EF⊥ME,
∴∠DME+∠GED=90°,
∵∠DAB=90°,
∴∠MDE+∠AED=90°,
∴∠AED=∠GED,
∵在△ADE和△GDE中,
 ,
,∴△ADE≌△GDE(AAS),
∴AD=GD,
∵
 的半径为DC,即AD的长度,
的半径为DC,即AD的长度,∴EF是
 所在⊙D的切线;
所在⊙D的切线;(2)MA=
 时,ME=MD=2-
时,ME=MD=2- =
= ,
,在Rt△AME中,AE=
 =
= =1,
=1,∴BE=AB-AE=2-1=1,
∵EF⊥ME,
∴∠1+∠2=180°-90°=90°,
∵∠B=90°,
∴∠2+∠3=90°,
∴∠1=∠3,
又∵∠DAB=∠B=90°,
∴△AME∽△BEF,
∴
 =
= ,
,即
 =
= ,
,
解得EF=
 ,
,在Rt△MEF中,MF=
 =
= =
= ;
;(3)假设△MFE能是等腰直角三角形,
则ME=EF,
∵在△AME和△BEF中,
 ,
,∴△AME≌△BEF(AAS),
∴MA=BE,
设AM=BE=x,
则MD=AD-MA=2-x,AE=AB-BE=2-x,
∵ME=MD,
∴ME=2-x,
∴ME=AE,
∵ME、AE分别是Rt△AME的斜边与直角边,
∴ME≠AE,
∴假设不成立,
故△MFE不能是等腰直角三角形.
点评:本题考查了圆的综合题型,主要考查了圆的切线的判定,全等三角形的判定与性质,相似三角形的判定与性质,勾股定理的应用,综合性较强,难度较大,(3)证明得到直角三角形的斜边与直角边相等的矛盾是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
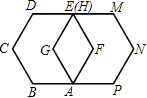 如图,如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合,那么点B的对应点是点
如图,如果边长为1的正六边形ABCDEF绕着顶点A顺时针旋转60°后与正六边形AGHMNP重合,那么点B的对应点是点 已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
 如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( )
如图,将边长为3的正六边形A1A2A3A4A5A6,在直线l上由图1的位置按顺时针方向向右作无滑动滚动,当A1第一次滚动到图2位置时,顶点A1所经过的路径的长为( ) 已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心,
已知:如图,在边长为a的正△ABC中,分别以A,B,C点为圆心, 长为半径作
长为半径作 ,
, ,
,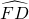 ,求阴影部分的面积.
,求阴影部分的面积. 长为半径作
长为半径作 ,
, ,
, ,求阴影部分的面积.
,求阴影部分的面积.