题目内容
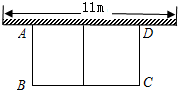 小莉的爸爸一面利用墙(墙的最大可用长度为11m),其余三面用长为40m的塑料网围成矩形鸡圈(其俯视图如图所示矩形ABCD),设鸡圈的一边AB长为xm,面积ym2.
小莉的爸爸一面利用墙(墙的最大可用长度为11m),其余三面用长为40m的塑料网围成矩形鸡圈(其俯视图如图所示矩形ABCD),设鸡圈的一边AB长为xm,面积ym2.(1)写出y与x的函数关系式;
(2)如果要围成鸡圈的面积为192m2的花圃,AB的长是多少?
(3)能围成比192m2更大的花圃吗?如果能,请求出最大面积;如果不能,请说明理由.
考点:二次函数的应用
专题:
分析:(1)利用矩形面积公式建立面积与AB的长的关系式;
(2)利用面积与AB的长的关系式在已知面积的情况下,求AB的长,由于是实际问题,AB的值也要受到限制;
(3)利用面积与AB的长的关系式求面积最大值.
(2)利用面积与AB的长的关系式在已知面积的情况下,求AB的长,由于是实际问题,AB的值也要受到限制;
(3)利用面积与AB的长的关系式求面积最大值.
解答:解:(1)由题意得:
矩形ABCD的面积=x(40-2x),即矩形ABCD的面积y=-2x2+40x.
(2)当矩形ABCD的面积为192时,-2x2+40x=192.
解此方程得x1=8,x2=12>11(不合题意,舍去).
∴当AB的长为8m时,花圃的面积为192m2.
(3)能.
矩形ABCD的面积=-2x2+40x=-2(x-10)2+200,
∵-2<0,
∴y有最大值,
∴当x=10时,y最大=200,
∴能围成比192m2更大的鸡棚,最大面积为200m2.
矩形ABCD的面积=x(40-2x),即矩形ABCD的面积y=-2x2+40x.
(2)当矩形ABCD的面积为192时,-2x2+40x=192.
解此方程得x1=8,x2=12>11(不合题意,舍去).
∴当AB的长为8m时,花圃的面积为192m2.
(3)能.
矩形ABCD的面积=-2x2+40x=-2(x-10)2+200,
∵-2<0,
∴y有最大值,
∴当x=10时,y最大=200,
∴能围成比192m2更大的鸡棚,最大面积为200m2.
点评:考查了一元二次方程的应用,根据题目的条件,合理地建立函数关系式,会判别函数关系式的类别,从而利用这种函数的性质解题.

练习册系列答案
相关题目
已知太阳的半径约为696000000m,则696000000这个数用科学记数法可表示为( )
| A、0.696×109 |
| B、6.96×109 |
| C、6.96×108 |
| D、69.6×107 |
已知三条线段长分别为a、b、c,a<b<c(a、b、c均为整数),若c=6,则线段a、b、c能组成三角形的情形有( )
| A、3种 | B、4种 | C、5种 | D、6种 |
下面的每组图形中,左面的平移后可以得到右面的是( )
A、 |
B、 |
C、 |
D、 |
在同一平面内,两条直线可能的位置关系是( )
| A、平行 | B、相交 |
| C、相交或平行 | D、垂直 |
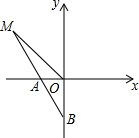 如图,M(m,n)为第二象限内一点,且m,n恰好为方程t2+2t+p=0的两个根,M点与原点的距离为2
如图,M(m,n)为第二象限内一点,且m,n恰好为方程t2+2t+p=0的两个根,M点与原点的距离为2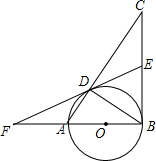 如图,在△ABC中,∠ABC=90°,AB=6,BC=8,以AB为直径的⊙O交AC于D,E是BC的中点,连接ED并延长交BA的延长线于点F.
如图,在△ABC中,∠ABC=90°,AB=6,BC=8,以AB为直径的⊙O交AC于D,E是BC的中点,连接ED并延长交BA的延长线于点F.