题目内容
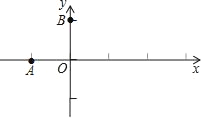
【题目】如图所示,在平面直角坐标系![]() 中,抛物线与
中,抛物线与![]() 轴相交于点
轴相交于点![]() ,点
,点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,
,![]() 与抛物线的对称轴相交于点
与抛物线的对称轴相交于点![]() .
.
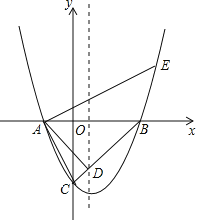
(1)求该抛物线的表达式,并直接写出点![]() 的坐标;
的坐标;
(2)过点![]() 作
作![]() 交抛物线于点
交抛物线于点![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,点![]() 在射线
在射线![]() 上,若
上,若![]() 与
与![]() 相似,求点
相似,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ,点
,点![]() ;(2)点
;(2)点![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)设抛物线的表达式为![]() ,将A、B、C三点坐标代入表达式,解出a、b、c的值即可得到抛物线表达式,同理采用待定系数法求出直线BC解析式,即可求出与对称轴的交点坐标;
,将A、B、C三点坐标代入表达式,解出a、b、c的值即可得到抛物线表达式,同理采用待定系数法求出直线BC解析式,即可求出与对称轴的交点坐标;
(2)过点E作EH⊥AB,垂足为H.先证∠EAH=∠ACO,则tan∠EAH=tan∠ACO=![]() ,设EH=t,则AH=2t,从而可得到E(-2+2t,t),最后,将点E的坐标代入抛物线的解析式求解即可;
,设EH=t,则AH=2t,从而可得到E(-2+2t,t),最后,将点E的坐标代入抛物线的解析式求解即可;
(3)先证明![]() ,再根据
,再根据![]() 与
与![]() 相似分两种情况讨论,建立方程求出AF,利用三角函数即可求出F点的坐标.
相似分两种情况讨论,建立方程求出AF,利用三角函数即可求出F点的坐标.
(1)设抛物线的表达式为![]() .
.
把![]() ,
,![]() 和
和![]() 代入得
代入得
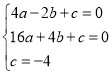 ,解得
,解得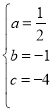 ,
,
![]() 抛物线的表达式
抛物线的表达式![]() ,
,
∴抛物线对称轴为![]()
设直线BC解析式为![]() ,
,
把![]() 和
和![]() 代入得
代入得
![]() ,解得
,解得![]()
∴直线BC解析式为![]()
当![]() 时,
时,![]()
![]() 点
点![]() .
.
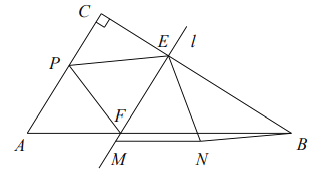
(2)如图,过点E作EH⊥AB,垂足为H.
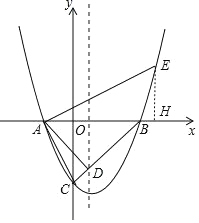
∵∠EAB+∠BAC=90°,∠BAC+∠ACO=90°,
∴∠EAH=∠ACO.
∴tan∠EAH=tan∠ACO=![]() .
.
设EH=t,则AH=2t,
∴点E的坐标为(2+2t,t).
将(2+2t,t)代入抛物线的解析式得:12(2+2t)2(2+2t)4=t,
解得:t=![]() 或t=0(舍去)
或t=0(舍去)
∴![]()
(3)如图所示,
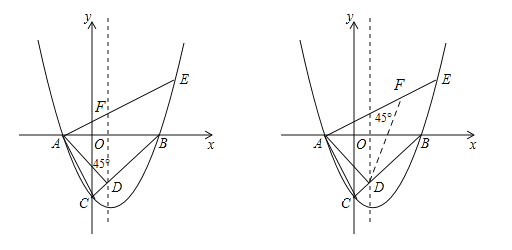
![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,
![]() .
.
由(2)中tan∠EAH=tan∠ACO可知![]() ,
,
![]() .
.
![]() 和
和![]() 相似,分两种情况讨论:
相似,分两种情况讨论:
①![]() ,即
,即![]() ,
,
![]() ,
,
∵tan∠EAB=![]()
∴sin∠EAB=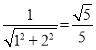
∴F点的纵坐标=![]()
![]() 点
点![]() .
.
②![]() ,即
,即![]() ,
,
![]() ,
,
同①可得F点纵坐标=![]()
横坐标=![]()
![]() 点
点![]() .
.
综合①②,点![]() 或
或![]() .
.

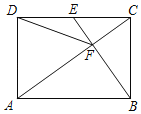
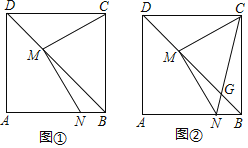
【题目】如图,在正方形![]() 中,
中,![]() ,点
,点![]() 在正方形边上沿
在正方形边上沿![]() 运动(含端点),连接
运动(含端点),连接![]() ,以
,以![]() 为边,在线段右侧作正方形
为边,在线段右侧作正方形![]() ,连接
,连接![]() 、
、![]() .
.
小颖根据学习函数的经验,在点![]() 运动过程中,对线段
运动过程中,对线段![]() 、
、![]() 、
、![]() 的长度之间的关系进行了探究.
的长度之间的关系进行了探究.
下面是小颖的探究过程,请补充完整:
(1)对于点![]() 在
在![]() 、
、![]() 边上的不同位置,画图、测量,得到了线段
边上的不同位置,画图、测量,得到了线段![]() 、
、![]() 、
、![]() 的长度的几组值,如下表:
的长度的几组值,如下表:
位置 | 位置 | 位置 | 位置 | 位置 | 位置 | 位置 | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
在![]() 、
、![]() 和
和![]() 的长度这三个量中,确定 的长度是自变量, 的长度和 的长度都是这个自变量的函数.
的长度这三个量中,确定 的长度是自变量, 的长度和 的长度都是这个自变量的函数.
(2)在同一平面直角坐标系![]() 中,画出(1)中所确定的函数的图象:
中,画出(1)中所确定的函数的图象:
(3)结合函数图像,解决问题:
当![]() 为等腰三角形时,
为等腰三角形时,![]() 的长约为
的长约为