题目内容
 如图,△ABC的外接圆上,AB,BC,CA三弧的度数比为12:13:11.自劣弧BC上取一点D,过D分别作直线AC,直线AB的平行线,且交
如图,△ABC的外接圆上,AB,BC,CA三弧的度数比为12:13:11.自劣弧BC上取一点D,过D分别作直线AC,直线AB的平行线,且交 |
| BC |
| A、55° | B、60° |
| C、65° | D、70° |
分析:先根据AB,BC,CA三弧的度数比为12:13:11求出
、
的度数,再根据其度数即可求出∠ACB及∠ABC的度数,由平行线的性质即可求出∠FED及∠EFD的度数,由三角形内角和定理即可求出∠EDF的度数.
 |
| AB |
 |
| AC |
解答:解:∵AB,BC,CA三弧的度数比为12:13:11,
∴
=
×360°=120°,
=
×360°=110°,
∴∠ACB=
×120°=60°,
∠ABC=
×110°=55°,
∵AC∥ED,AB∥DF,
∴∠FED=∠ACB=60°,
∠EFD=∠ABC=55°,
∴∠EDF=180°-60°-55°=65°.
故选C.
∴
 |
| AB |
| 12 |
| 12+13+11 |
 |
| AC |
| 11 |
| 12+13+11 |
∴∠ACB=
| 1 |
| 2 |
∠ABC=
| 1 |
| 2 |
∵AC∥ED,AB∥DF,
∴∠FED=∠ACB=60°,
∠EFD=∠ABC=55°,
∴∠EDF=180°-60°-55°=65°.
故选C.
点评:本题考查的是圆心角、弧、弦的关系及平行线的性质,能根据AB,BC,CA三弧的度数比为12:13:11求出∠ABC及∠ACB的度数是解答此题的关键.

练习册系列答案
相关题目
 如图,半圆O为△ABC的外接半圆,AC为直径,D为劣弧
如图,半圆O为△ABC的外接半圆,AC为直径,D为劣弧 (2013•沙湾区模拟)如图,△ABC的外接⊙O的半径为R,高为AD,∠BAC的平分线交⊙O、BC于E、P,EF切⊙O交AC的延长线于F.
(2013•沙湾区模拟)如图,△ABC的外接⊙O的半径为R,高为AD,∠BAC的平分线交⊙O、BC于E、P,EF切⊙O交AC的延长线于F. 如图,⊙O是△ABC的
如图,⊙O是△ABC的 如图,△ABC的外接⊙O的半径为R,高为AD,∠BAC的平分线交⊙O、BC于E、P,EF切⊙O交AC的延长线于F.
如图,△ABC的外接⊙O的半径为R,高为AD,∠BAC的平分线交⊙O、BC于E、P,EF切⊙O交AC的延长线于F.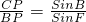 .
. 如图,△ABC的外接⊙O的半径为R,高为AD,∠BAC的平分线交⊙O、BC于E、P,EF切⊙O交AC的延长线于F.
如图,△ABC的外接⊙O的半径为R,高为AD,∠BAC的平分线交⊙O、BC于E、P,EF切⊙O交AC的延长线于F. .
.