题目内容
 如图,已知D是△ABC中的边BC上的一点,∠BAD=∠C,∠ABC的平分线交边AC于E,交AD于F,那么下列结论中错误的是
如图,已知D是△ABC中的边BC上的一点,∠BAD=∠C,∠ABC的平分线交边AC于E,交AD于F,那么下列结论中错误的是
- A.△BAC∽△BDA
- B.△BFA∽△BEC
- C.△BDF∽△BEC
- D.△BDF∽△BAE
C
分析:根据相似三角形的判定,采用排除法,逐项分析判断.
解答:∵∠BAD=∠C,
∠B=∠B,
∴△BAC∽△BDA.故A正确.
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴△BFA∽△BEC.故B正确.
∴∠BFA=∠BEC,
∴∠BFD=∠BEA,
∴△BDF∽△BAE.故D正确.
而不能证明△BDF∽△BEC,故C错误.
故选C.
点评:本题考查相似三角形的判定.识别两三角形相似,除了要掌握定义外,还要注意正确找出两三角形的对应边和对应角.
分析:根据相似三角形的判定,采用排除法,逐项分析判断.
解答:∵∠BAD=∠C,
∠B=∠B,
∴△BAC∽△BDA.故A正确.
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴△BFA∽△BEC.故B正确.
∴∠BFA=∠BEC,
∴∠BFD=∠BEA,
∴△BDF∽△BAE.故D正确.
而不能证明△BDF∽△BEC,故C错误.
故选C.
点评:本题考查相似三角形的判定.识别两三角形相似,除了要掌握定义外,还要注意正确找出两三角形的对应边和对应角.

练习册系列答案
相关题目
 16、如图,已知O是AB的中点,再加上什么条件,能使△AOC和△BOD全等?为什么?
16、如图,已知O是AB的中点,再加上什么条件,能使△AOC和△BOD全等?为什么?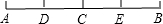
 如图,已知M是AB的中点,N是AC的中点,若MN=5cm,则BC=
如图,已知M是AB的中点,N是AC的中点,若MN=5cm,则BC= 如图,已知M是AB的中点,AC∥MD,AC=MD,试说明下面结论成立的理由:(1)△ACM≌△MDB;(2)CM=DB,CM∥DB.
如图,已知M是AB的中点,AC∥MD,AC=MD,试说明下面结论成立的理由:(1)△ACM≌△MDB;(2)CM=DB,CM∥DB. 如图,已知M是AB的中点,下面哪个结论不是根据“M是AB的中点”推出来的( )
如图,已知M是AB的中点,下面哪个结论不是根据“M是AB的中点”推出来的( )