Question

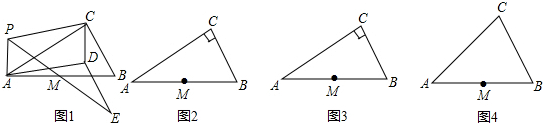
如图（1），Rt△ABC中，∠ACB=90°，中线BE、CD相交于点O，点F、G分别是OB、OC的中点．
（1）求证：四边形DFGE是平行四边形；
（2）如果把Rt△ABC变为任意△ABC，如图（2），通过你的观察，第（1）问的结论是否仍然成立（不用证明）；
（3）在图（2）中，试想：如果拖动点A，通过你的观察和探究，在什么条件下四边形DFGE是矩形，并给出证明；
（4）在第（3）问中，试想：如果拖动点A，是否存在四边形DFGE是正方形或菱形？如果存在，画出相应的图形（不用证明）．

Answer 1

分析：（1）（2）由于DE是△ABC的中位线，有DE平行于BC，且等于BC的一半，同理FG是△OBC的中位线，有FG平行于BC，且等于BC的一半，故有DE与FG平行且相等，有四边形DFGE是平行四边形．
（3）当AB=AC时，四边形DFGE是矩形，可由等腰三角形的三线合一的性质得到DF⊥FG．

解答：证明：（1）∵BE、CD是中线，
∴D、E是两边的中点．
∴DE∥BC且DE=

1

2

BC．（1分）
又∵点F、G分别是OB、OC的中点，
∴FG∥BC且FG=

1

2

BC．
∴DE∥FG且DE=FG．
∴四边形DFGE是平行四边形．（1分）

解：（2）成立．（1分）

（3）如图，当AB=AC时，四边形DFGE是矩形（1分）
作AH⊥BC，如图所示，
∵AB=AC，AH⊥BC
∴AH是BC边的中线，
又∵BE、CD是中线，
∴AH必过点O．（三角形三条中线相交于一点）（1分）
∵DF为△ABO的中位线，
∴DF∥AO，即DF∥AH，
又∵FG为△BCO的中位线，
∴FG∥BC，
又∵FG∥BC，AH⊥BC，
∴AH⊥FG．
∴∠DFG=90度．
又∵四边形DFGE是平行四边形，
∴四边形DFGE是矩形．（1分）

（4）解：拖动点A，存在四边形DFGE是正方形或菱形，如图所示．（1分）

点评：本题利用了三角形的中位线的性质，等腰三角形的性质求解．同时此题是一道几何结论动态题，可以大大激发学生的思考兴趣，拓展学生的思维空间，培养学生求异、求变的创新精神．