题目内容
【题目】如图,线段AB=1,点P是线段AB上一个动点(不包括A、B)在AB同侧作Rt△PAC,Rt△PBD,∠A=∠D=30°,∠APC=∠BPD=90°,M、N分别是AC、BD的中点,连接MN,设AP=x,MN2=y,则y关于x的函数图象为( )
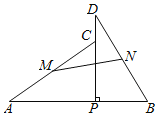
A. 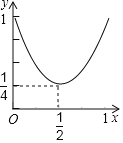 B.
B. 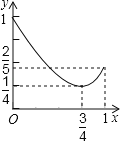
C. 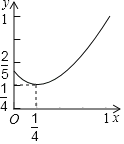 D.
D. 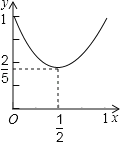
【答案】B
【解析】
连接PM、PN,则PM、PN分别为Rt△PAC,Rt△PBD的中线,则∠A=∠D=30°,则∠MAP=∠A=30°,则PM= =
=![]() ,PN=
,PN= =1﹣x,即可求解.
=1﹣x,即可求解.
解:连接PM、PN,则PM、PN分别为Rt△PAC,Rt△PBD的中线,

∵∠A=∠D=30°,则∠MAP=∠A=30°,
则PM= =
=![]() ,
,
同理PN= =1﹣x,
=1﹣x,
y=MN2=(PM)2+(PN)2=![]() x2﹣2x+1,
x2﹣2x+1,
函数的对称轴x=﹣![]() =
=![]() ,
,
故选:B.

练习册系列答案
相关题目
【题目】如图,已知反比例函数y=![]() (x<0)的图象经过OABC的顶点B,点A在x轴上,AC⊥x轴交反比例函数图象于点D,BE⊥x轴于点E,则BE:AD=( )
(x<0)的图象经过OABC的顶点B,点A在x轴上,AC⊥x轴交反比例函数图象于点D,BE⊥x轴于点E,则BE:AD=( )
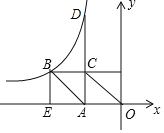
A. 1:2B. 1:![]() C. 1:3D. 1:
C. 1:3D. 1:![]()
【题目】已知二次函数![]() ,
,![]() 与
与![]() 的部分对应值如下表所示:
的部分对应值如下表所示:
| … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| … | 6 | 1 | -2 | -3 | -2 | m | … |
下面有四个论断:
①抛物线![]() 的顶点为
的顶点为![]() ;
;
②![]() ;
;
③关于![]() 的方程
的方程![]() 的解为
的解为![]() ;
;
④![]() .
.
其中,正确的有___________________.