题目内容
 如图,在矩形ABCD中,点E为AB的中点,EF⊥EC交AD于点F,连接CF(AD>AE),下列结论:
如图,在矩形ABCD中,点E为AB的中点,EF⊥EC交AD于点F,连接CF(AD>AE),下列结论:①∠AEF=∠BCE; ②S△CEF=S△EAF+S△CBE;
③AF+BC>CF; ④若
| BC |
| CD |
| ||
| 2 |
其中正确的结论是
考点:全等三角形的判定与性质,矩形的性质
专题:
分析:延长CB,FE交于点G,易证∠AEF=∠BCE,可得①正确;
即可证明△AEF≌△BEG,可得AF=BG,EF=EG,即可求得S△CEF=S△EAF+S△CBE,可得②正确;
可得AF+BC=CF,即可得③错误;
易证∠BCE=30°,即可证明△CEF≌△CDF,可得④正确,即可解题.
即可证明△AEF≌△BEG,可得AF=BG,EF=EG,即可求得S△CEF=S△EAF+S△CBE,可得②正确;
可得AF+BC=CF,即可得③错误;
易证∠BCE=30°,即可证明△CEF≌△CDF,可得④正确,即可解题.
解答:解:延长CB,FE交于点G,
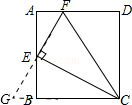
∵∠AEF+∠BEC=90°,∠BEC+∠BCE=90°,
∴∠AEF=∠BCE,①正确;
在△AEF和△BEG中,
,
∴△AEF≌△BEG(ASA),
∴AF=BG,EF=EG,
∵CE⊥EG,
∴S△CEG=S△CEF,CG=CF,
∴S△CEF=S△EAF+S△CBE,②正确;
∴AF+BC=BG+BC=CG=CF,③错误;
∵
=
,
∴∠BCE=30°,∴∠FCE=∠FCD=30°,
在△CEF和△CDF中,
,
∴△CEF≌△CDF(AAS),④正确.
故答案为:①②④.

∵∠AEF+∠BEC=90°,∠BEC+∠BCE=90°,
∴∠AEF=∠BCE,①正确;
在△AEF和△BEG中,
|
∴△AEF≌△BEG(ASA),
∴AF=BG,EF=EG,
∵CE⊥EG,
∴S△CEG=S△CEF,CG=CF,
∴S△CEF=S△EAF+S△CBE,②正确;
∴AF+BC=BG+BC=CG=CF,③错误;
∵
| BC |
| CD |
| ||
| 2 |
∴∠BCE=30°,∴∠FCE=∠FCD=30°,
在△CEF和△CDF中,
|
∴△CEF≌△CDF(AAS),④正确.
故答案为:①②④.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△AEF≌△BEG和△CEF≌△CDF是解题的关键.

练习册系列答案
相关题目
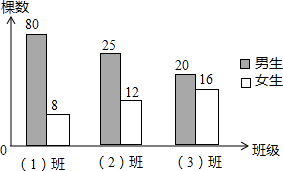 为了绿化环境,七年级(1)(2)(3)班参加植树造林活动,已知男同学4人每天植5棵树,女同学5人每天植4棵,如图统计图描述了三个班一天植树的棵树情况,则参加植树人数最多的班级是
为了绿化环境,七年级(1)(2)(3)班参加植树造林活动,已知男同学4人每天植5棵树,女同学5人每天植4棵,如图统计图描述了三个班一天植树的棵树情况,则参加植树人数最多的班级是 若函数y=-x2+2x+k的部分图象如图所示,由图可知,关于x的方程-x2+2x+k=0的一根是3,则另一根为
若函数y=-x2+2x+k的部分图象如图所示,由图可知,关于x的方程-x2+2x+k=0的一根是3,则另一根为 一渔船在海岛A南偏东20°方向的B处遇险,测得海岛A与B的距离为20
一渔船在海岛A南偏东20°方向的B处遇险,测得海岛A与B的距离为20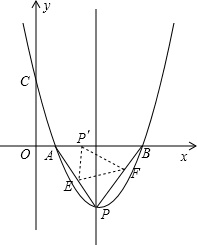 已知:抛物线经过A(2,0)、B(8,0)、C(0,
已知:抛物线经过A(2,0)、B(8,0)、C(0,