Question

【题目】在中，是边上一点，将绕着点逆时针旋转至，连接．

（1）如图1，连接，当时，，若，，，求线段的长．

（2）如图2，连接交于点，若，点为中点，求证：．

Answer 1

【答案】（1）6；（2）证明见解析

【解析】

（1）由勾股定理可求DF=，由旋转的性质可得DF=CD=AB=，由勾股定理可求BE的长；

（2）过点A作AH∥DE，交FD的延长线于点H，由平行四边形的性质和平行线的性质可得∠H=∠C，∠HAD=∠DEC，由平行线分线段成比例定理可得HD=DF，由中位线可得AH=2DG，由“AAS”可证△AHD≌△ECD，可得AH=EC，即可得结论．

（1）∵∠ADF=90°，，

∴DF=

∵将CD绕着点D逆时针旋转至DF，

∴DF=CD=

∵四边形ABCD是平行四边形，

∴AB=CD=

∵AE=2BE，且AB2=AE2+BE2，

∴180=5BE2，

∴BE=6

故答案为：6

（2）如图2，过点A作AH∥DE，交FD的延长线于点H，

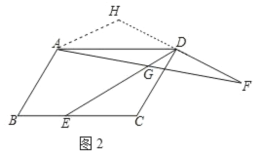
∴∠HAD=∠ADE，∠H=∠EDF，

∵四边形ABCD是平行四边形，

∴AD∥BC，AB∥CD

∴∠B+∠C=180°，∠ADE=∠DEC，

∴∠HAD=∠DEC，

∵∠EDF+∠B=180°，

∴∠H=∠EDF=∠C，

∵DG∥AH，

∴，且AG=GF

∴HD=DF

∴HD=DF=CD，且AG=GF，

∴AH=2DG，

∵DH=DC，∠H=∠C，∠HAD=∠DEC，

∴△AHD≌△ECD（AAS），

∴AH=EC，

∴EC=2DG，

∴BE=BC-EC=AD-2DG．