题目内容
 如图,△ABC的外接圆⊙O的半径为1,D、E分别为AB、AC的中点,BF为高,若AB=
如图,△ABC的外接圆⊙O的半径为1,D、E分别为AB、AC的中点,BF为高,若AB= ,则线段BF的长等于
,则线段BF的长等于
- A.2DE
- B.
 DE
DE - C.AF
- D.
 AE
AE
B
分析:此题需要将∠BAC转化到直角三角形中进行求解,连接AO和BO,利用勾股定理逆定理可以判定∠AOB=90°,然后利用圆周角定理得到∠C=45°,得到△BFC为等腰直角三角形,从而得到BF于BC的关系,进而得到BF与DE的关系.
解答: 解:如图,连接AO、BO,
解:如图,连接AO、BO,
∵△ABC的外接圆⊙O的半径为1,
∴OA=OB=1,
∵AB= ,
,
∴△ABO为直角三角形,
∴∠AOB=90°,
∴∠ACB=45°,
∵BF为高,
∴BF= ,
,
∵D、E分别为AB、AC的中点,
∴BC=2DE
∴BF= =
= =
= ,
,
故选B.
点评:此题主要考查了三角形的外接圆、圆周角定理、锐角三角函数的定义以及相似三角形的判定和性质等知识,正确地构造出直角三角形是解题的关键.
分析:此题需要将∠BAC转化到直角三角形中进行求解,连接AO和BO,利用勾股定理逆定理可以判定∠AOB=90°,然后利用圆周角定理得到∠C=45°,得到△BFC为等腰直角三角形,从而得到BF于BC的关系,进而得到BF与DE的关系.
解答:
 解:如图,连接AO、BO,
解:如图,连接AO、BO,∵△ABC的外接圆⊙O的半径为1,
∴OA=OB=1,
∵AB=
 ,
,∴△ABO为直角三角形,
∴∠AOB=90°,
∴∠ACB=45°,
∵BF为高,
∴BF=
 ,
,∵D、E分别为AB、AC的中点,
∴BC=2DE
∴BF=
 =
= =
= ,
,故选B.
点评:此题主要考查了三角形的外接圆、圆周角定理、锐角三角函数的定义以及相似三角形的判定和性质等知识,正确地构造出直角三角形是解题的关键.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
 如图,半圆O为△ABC的外接半圆,AC为直径,D为劣弧
如图,半圆O为△ABC的外接半圆,AC为直径,D为劣弧
 (2013•沙湾区模拟)如图,△ABC的外接⊙O的半径为R,高为AD,∠BAC的平分线交⊙O、BC于E、P,EF切⊙O交AC的延长线于F.
(2013•沙湾区模拟)如图,△ABC的外接⊙O的半径为R,高为AD,∠BAC的平分线交⊙O、BC于E、P,EF切⊙O交AC的延长线于F. 如图,⊙O是△ABC的
如图,⊙O是△ABC的 如图,△ABC的外接⊙O的半径为R,高为AD,∠BAC的平分线交⊙O、BC于E、P,EF切⊙O交AC的延长线于F.
如图,△ABC的外接⊙O的半径为R,高为AD,∠BAC的平分线交⊙O、BC于E、P,EF切⊙O交AC的延长线于F.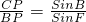 .
. 如图,△ABC的外接⊙O的半径为R,高为AD,∠BAC的平分线交⊙O、BC于E、P,EF切⊙O交AC的延长线于F.
如图,△ABC的外接⊙O的半径为R,高为AD,∠BAC的平分线交⊙O、BC于E、P,EF切⊙O交AC的延长线于F. .
.