Question

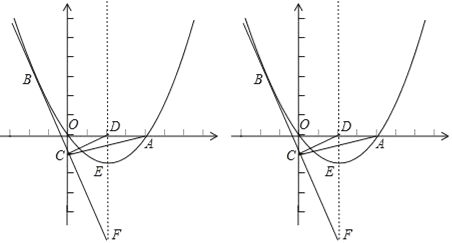
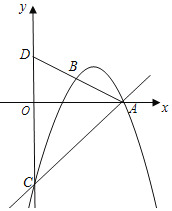
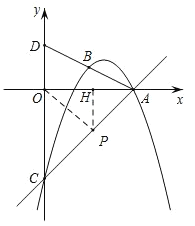
【题目】如图，抛物线y=ax2+4x+c过点A(6，0)、B(3，)，与y轴交于点C．联结AB并延长，交y轴于点D．

(1)求该抛物线的表达式；

(2)求△ADC的面积；

(3)点P在线段AC上，如果△OAP和△DCA相似，求点P的坐标．

Answer 1

【答案】(1)y=-x2+4x-6；(2)S△ADC=27；(3)点P的坐标为(2，-4)或(，-)．

【解析】

(1)将A(6，0)，B(3，)代入y=ax2+4x+c，即可求出a，c值，进一步写出抛物线解析式；

(2)分别求抛物线，直线与坐标轴交点D，C的坐标，可直接求出△ADC的面积；

(3)先求出∠OAC=∠OCA=45°，再分类讨论△OAP和△DCA相似的两种情况，求出AP长度，可利用特殊角进一步求出相关线段的长度，即可写出点P的坐标．

解：(1)将A(6，0)，B(3，)代入y=ax2+4x+c，

得，，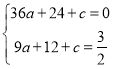

解得，a=-，c=-6，

∴该抛物线解析式为：y=-x2+4x-6；

(2)将A(6，0)，B(3，)代入y=kx+b，

得，，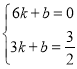

解得，k=-，b=3，

∴yAB=-x+3，

当x=0时，y=3，

∴D(0，3)，OD=3，

在抛物线y=-x2+4x-6中，

当x=0时，y=-6，

∴C(0，-6)，OC=6，

∴DC=OC+OD=9，

∵A(6，0)，

∴OA=6，

∴S△ADC=DCOA=27；

(3)由(2)知，OC=OA=6，

∴△AOC为等腰直角三角形，

∴∠OAC=∠OCA=45°，AC=OA=6，

如图所示，连接OP，过点P作PH⊥OA于H，

则△PHA为等腰直角三角形，

①当△DCA∽OAP时，

=，

即=，

∴AP=4，

∴HP=HA=AP=4，OH=OA-HA=2，

∴P(2，-4)；

②当△DCA∽△PAO时，

=，

即=，

∴PA=，

∴HP=HA=，

∴OH=OA-AH=，

∴P(，-)，

综上所述，点P的坐标为(2，-4)或(，-)．