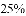题目内容
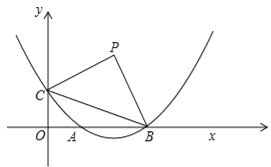
(题文)如图,已知抛物线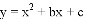 经过
经过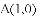
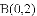
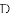
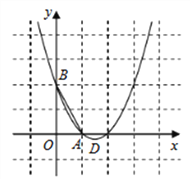
(1)求抛物线的解析式;
(2)将
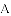
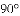
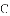
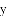
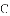
(3)设(2)中平移后,所得抛物线与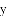
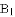 ,顶点为
,顶点为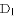 ,若点
,若点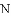
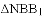 的面积是
的面积是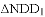 面积的2倍,求点
面积的2倍,求点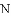
练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
很多运动员为了参加北京—张家口冬季奥运会,进行了积极的训练.下表记录了国家队4名队员在500米短道速滑训练成绩的平均数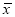 与方差
与方差 :
:
队员甲 | 队员乙 | 队员丙 | 队员丁 | |
平均数 | 45 | 46 | 45 | 46 |
方差 | 1.5 | 1.5 | 3.5 | 4.5 |
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A. 队员甲 B. 队员乙 C. 队员丙 D. 队员丁
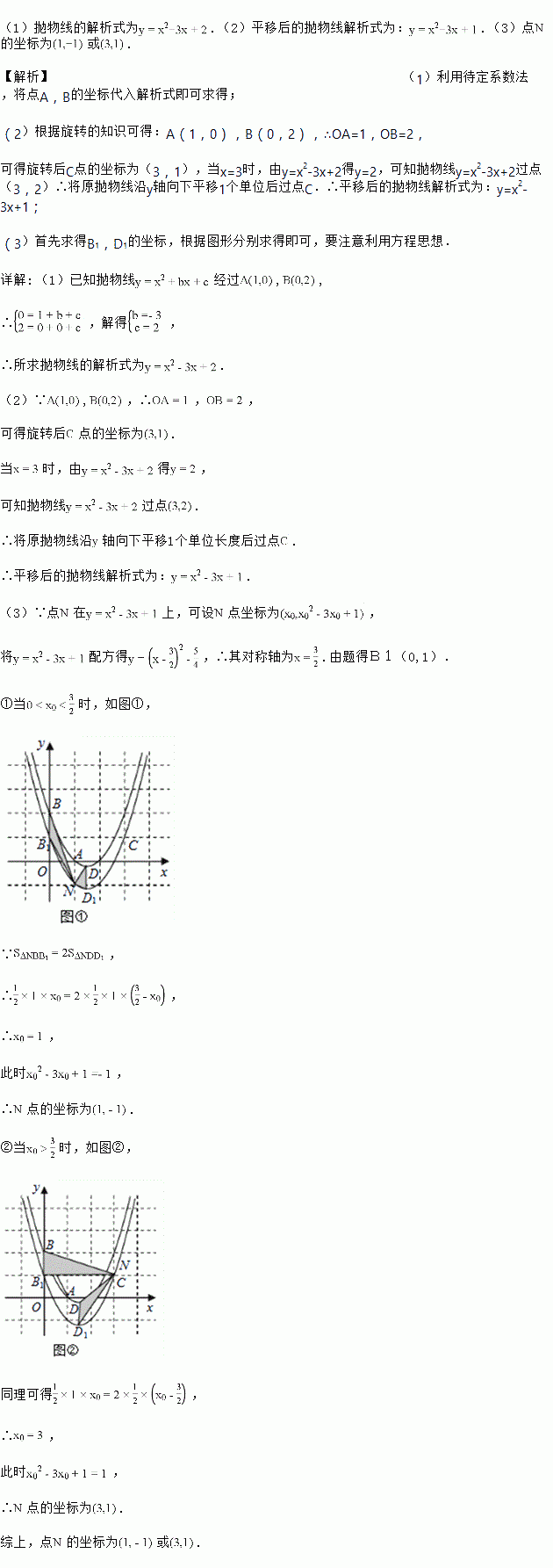

 (x>0)与△ABC总有公共点,则k的取值范围是________.
(x>0)与△ABC总有公共点,则k的取值范围是________.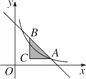
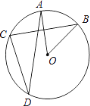
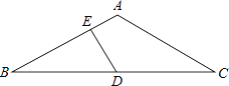
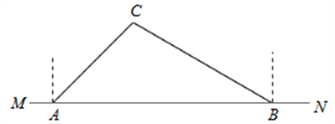
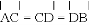 ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=
,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED= ∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )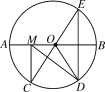
 (秒)
(秒) (秒2)
(秒2)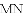
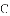
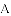
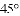
 )
)