题目内容
 如图1,在边长为2的等边△ABC中,⊙A与BC相切于点D,阴影部分的面积记作S1;如图2,最大圆半径r=1,阴影部分的面积记作S2,则S1与S2的大小关系是( )
如图1,在边长为2的等边△ABC中,⊙A与BC相切于点D,阴影部分的面积记作S1;如图2,最大圆半径r=1,阴影部分的面积记作S2,则S1与S2的大小关系是( )| A、S1>S2 |
| B、S1<S2 |
| C、S1=S2 |
| D、无法确定 |
考点:旋转的性质
专题:计算题
分析:由⊙A与BC相切于点D,根据切线的性质得AD⊥BC,则利用等边三角形的性质得BD=CD=1,AD平分∠BAC,∠BAC=60°,∠BAD=∠CAD=30°,于是可计算出AD=
BD=
,利用旋转可把阴影部分合成△ABD,所以S1=S△ABD=
;如图2,利用旋转,可把阴影部分合成最大圆的
,则根据圆的面积公式得到S2=
S大圆=
,然后比较大小即可.
| 3 |
| 3 |
| ||
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| π |
| 4 |
解答:解:如图1,∵⊙A与BC相切于点D,
∴AD⊥BC,
∵△ABC为等边三角形,
∴BD=CD=1,AD平分∠BAC,∠BAC=60°,
∴∠BAD=∠CAD=30°,
∴AD=
BD=
,
∴S1=S△ABD=
×1×
=
,
如图2,S2=
S大圆=
•π•12=
,
=
>
,
∴S1>S2.
故选A.
∴AD⊥BC,
∵△ABC为等边三角形,
∴BD=CD=1,AD平分∠BAC,∠BAC=60°,
∴∠BAD=∠CAD=30°,
∴AD=
| 3 |
| 3 |
∴S1=S△ABD=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
如图2,S2=
| 1 |
| 4 |
| 1 |
| 4 |
| π |
| 4 |
| ||
| 2 |
2
| ||
| 4 |
| π |
| 4 |
∴S1>S2.
故选A.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等边三角形的性质.把几个不规则的图形利用旋转得到一个规则的图形是解决此题的关键.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
在电视访谈节目中,一位气象专家说“本地区未来10天内发生降水的概率是三分之二”,以下哪个选项最能反映气象专家的意思( )
| A、这个地区从现在开始经过6至7天会发生降水 |
| B、这个地区未来10天内将会发生一次降水 |
| C、这个地区未来10天内发生降水比不发生降水的可能性大 |
| D、我们不能判断何时会有降水发生 |
下列调查方式,你认为最合适的是( )
| A、日光灯管厂要检测一批灯管的使用寿命,采用普查方式 |
| B、了解海门市每天的流动人口数,采用抽样调查方式 |
| C、了解海门市民对各类电视节目的喜爱情况,采用普查方式 |
| D、旅客上飞机前的安检,采用抽样调查方式 |
 二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法中错误的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法中错误的是( )| A、函数有最小值 | ||
| B、当-1<x<2时,y>0 | ||
C、当x<
| ||
D、对称轴是直线x=
|
 已知:如图,点A,B,C,D在一条直线上,AB=CD,AE∥FD,且∠E=∠F.求证:EC=FB.
已知:如图,点A,B,C,D在一条直线上,AB=CD,AE∥FD,且∠E=∠F.求证:EC=FB. 如图,梯形ABCD中,AB∥CD,∠BCD=90°,CD=8,AD=13.将该梯形沿BD翻折,使点C恰好与边AD上点E重合,那么BC=
如图,梯形ABCD中,AB∥CD,∠BCD=90°,CD=8,AD=13.将该梯形沿BD翻折,使点C恰好与边AD上点E重合,那么BC=
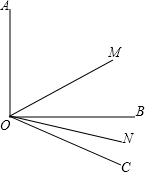 已知如图,OM平分∠AOC,ON平分∠BOC,若∠AOB=90°,∠BOC=30°
已知如图,OM平分∠AOC,ON平分∠BOC,若∠AOB=90°,∠BOC=30°